题目内容
某商品进货价每件50元,据市场调查,当销售价格(每件x元)在50<x≤80时,每天售出的件数P=
解法一:设销售价定为每件x元(50<x≤80).
每天获得利润y元,则y=(x-50)·P=![]() .
.
设x-50=t,则0<t≤30,
∴y=![]() =
=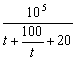 ≤
≤![]() =2500.
=2500.
当且仅当t=10,即x=60时,ymax=2500.
答:每件60元时,每天获利最多,最多是2500元.
解法二:求y=![]() 的最大值,还可转化为二次函数的最大值问题解之.
的最大值,还可转化为二次函数的最大值问题解之.
令![]() =t,∵10<x-40≤40,∴
=t,∵10<x-40≤40,∴![]() ≤t<
≤t<![]() .
.
y=![]() =105·t2(
=105·t2(![]() -10)=105(-10t2+t).
-10)=105(-10t2+t).
当t=![]() ,即x=60时,ymax=2500.
,即x=60时,ymax=2500.
求y的最大值,还可以用二次函数的判别式方法解.
令x-40=t,则10<t≤40,y=![]() ,
,
即yt2-105t+106=0. ①
Δ=1010-4·106·y≥0.
解之y≤2500,即ymax=2500.
检验:当y=2500时,方程①2500t2-105t+106=0,即t2-40t+400=0.
解之t=20∈(10,40].
这时x=60.
点评:(1)设变量时,把最值变量定为函数,建立函数关系式.(2)构造相应的数学模型求最值.法一:令x-50=t,使分子最简,同除以分子后,很容易用均值不等式求分母的最值.法二:令![]() =t,使二次函数式最简,易于求二次函数y的最值.法三:令x-40=t,应用二次方程判别式求最值.但应注意检验.
=t,使二次函数式最简,易于求二次函数y的最值.法三:令x-40=t,应用二次方程判别式求最值.但应注意检验.

练习册系列答案
相关题目
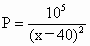 ,若想每天获得的利润最多,销售价格每件应定为多少元?
,若想每天获得的利润最多,销售价格每件应定为多少元?
 ,若想每天获得的利润最多,销售价格每件应定为多少元?
,若想每天获得的利润最多,销售价格每件应定为多少元? ,若要使每天获得的利润最多,销售价格每件应定为多少元?
,若要使每天获得的利润最多,销售价格每件应定为多少元?