题目内容
5.已知双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1,则直线y=$\frac{\sqrt{3}}{2}$x与C有0个公共点;若直线y=k(x-3)与C只有一个公共点.则k取值范围为{-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$}.分析 求得双曲线的渐近线方程,考虑与渐近线平行的直线的特点,求得直线y=k(x-3恒过定点(3,0),即可得到所求范围.
解答 解:双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1的渐近线方程为y=±$\frac{\sqrt{3}}{2}$x,
即有直线y=$\frac{\sqrt{3}}{2}$x与C没有公共点;
直线y=k(x-3)恒过定点(3,0),
由(3,0)在双曲线的右支开口之内,
则只有过(3,0)的直线与渐近线平行,与双曲线只有一个公共点,
故k=±$\frac{\sqrt{3}}{2}$.
故答案为:0,{-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$}.
点评 本题考查双曲线的渐近线方程及应用,考查直线恒过定点的求法,以及直线和双曲线的位置关系,属于基础题.

练习册系列答案
相关题目
16.已知直线y=k(x+a)(a>0)与x轴交于点A,与直线x=c(c>0,c<a)交于点M,椭圆C以A为左顶点,以F(c,0)为右焦点,且过点M,当$\frac{1}{3}$<k<$\frac{1}{2}$时,椭圆C的离心率的范围是( )
| A. | $(0,\frac{2}{3})$ | B. | $(\frac{2}{3},1)$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{1}{2},\frac{2}{3})$ |
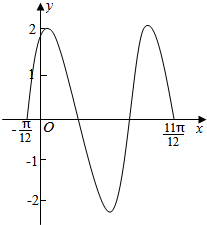 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示:
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示: