题目内容
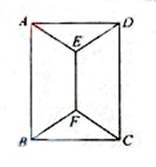
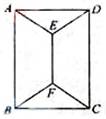
如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用 种.
【答案】
168.
【解析】按照用三种颜色还是四种颜色分两类
若用三种颜色,则是AF,BD,EC各用一种颜色,共 种;
种;
若用四种颜色,先用三种颜色涂A,B,D三点,E,C颜色可同可不同,当E,C颜色相同时,共 种;当E,C颜色不同时,共
种;当E,C颜色不同时,共 种.所以不同的涂色方法共有24+48+96=168种.
种.所以不同的涂色方法共有24+48+96=168种.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
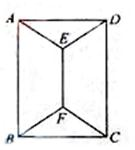 11、如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用( )
11、如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用( )