题目内容
如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
(A)288种 (B)264种 (C)240种 (D)168种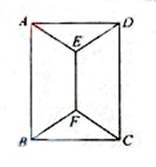
【答案】D
【解析】本题主要考查排列组合的基础知识与分类讨论思想,属于难题。
B,D,E,F用四种颜色,则有![]() 种涂色方法;
种涂色方法;
B,D,E,F用三种颜色,则有![]() 种涂色方法;
种涂色方法;
B,D,E,F用两种颜色,则有![]() 种涂色方法;
种涂色方法;
所以共有24+192+48=264种不同的涂色方法。
【温馨提示】近两年天津卷中的排列、组合问题均处理压轴题的位置,且均考查了分类讨论思想及排列、组合的基本方法,要加强分类讨论思想的训练。

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
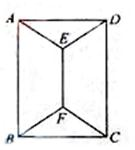 11、如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用( )
11、如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用( )

