题目内容
已知f(x)= sinxcosx-cos2x-
sinxcosx-cos2x- ,x∈R。
,x∈R。
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的三内角A,B,C对边分别为a,b,c且c=3,f(C)=0,若向量 =(1,sinA)与
=(1,sinA)与 =(2,sinB)共线,求a,b的值。
=(2,sinB)共线,求a,b的值。
 sinxcosx-cos2x-
sinxcosx-cos2x- ,x∈R。
,x∈R。(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的三内角A,B,C对边分别为a,b,c且c=3,f(C)=0,若向量
 =(1,sinA)与
=(1,sinA)与 =(2,sinB)共线,求a,b的值。
=(2,sinB)共线,求a,b的值。解:(1)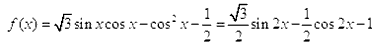
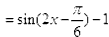
∴f(x)的最小值为-2,最小正周期为π;
(2)∵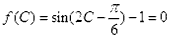 ,即
,即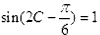
因为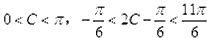
∴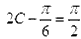
∴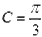
因为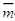 与
与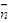 共线
共线
∴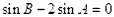
由正弦定理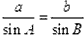 得
得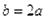 ①
①
∵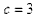 ,由余弦定理,得
,由余弦定理,得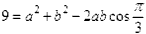 ②
②
解方程组①②,得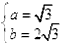 。
。
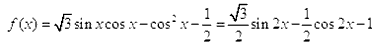
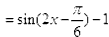
∴f(x)的最小值为-2,最小正周期为π;
(2)∵
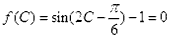 ,即
,即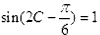
因为
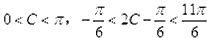
∴
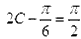
∴
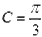
因为
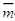 与
与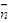 共线
共线∴
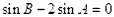
由正弦定理
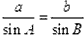 得
得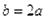 ①
①∵
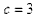 ,由余弦定理,得
,由余弦定理,得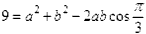 ②
②解方程组①②,得
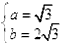 。
。
练习册系列答案
相关题目
已知f(x)=sin(x+
),g(x)=cos(x-
),则f(x)的图象( )
| π |
| 2 |
| π |
| 2 |
| A、与g(x)的图象相同 | ||
| B、与g(x)的图象关于y轴对称 | ||
C、向左平移
| ||
D、向右平移
|