题目内容
17.已知A、B、C三点在球O的球面上,AB=BC=CA=3,且球心O到平面ABC的距离等于球半径的$\frac{1}{3}$,则球O的表面积为( )| A. | 12π | B. | 16π | C. | 18π | D. | $\frac{27π}{2}$ |
分析 设出球的半径,小圆半径,通过已知条件求出两个半径,再求球的表面积.
解答 解:设球的半径为r,O′是△ABC的外心,外接圆半径为R=$\sqrt{3}$,
∵球心O到平面ABC的距离等于球半径的$\frac{1}{3}$,
∴得r2-$\frac{1}{9}$r2=3,得r2=$\frac{27}{8}$.
球的表面积S=4πr2=4π×$\frac{27}{8}$=$\frac{27}{2}$π.
故选:D.
点评 本题考查球O的表面积,考查学生分析问题解决问题能力,空间想象能力,是中档题.

练习册系列答案
相关题目
7.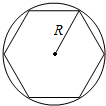 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )| A. | $\frac{3}{2π}$ | B. | $\frac{3\sqrt{3}}{2π}$ | C. | $\frac{3}{4π}$ | D. | $\frac{3\sqrt{3}}{4π}$ |
8.若p∨q为真命题,则下列结论不可能成立的是( )
| A. | p真q真 | B. | p假q真 | C. | p真q假 | D. | p假q假 |
9.下列向量组中,能作为它们所在平面内所有向量的基底的是( )
| A. | $\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(0,0) | B. | $\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,-4) | C. | $\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(3,6) | D. | $\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,2) |
6.已知满足条件x2+y2≤1的点(x,y)构成的平面区域的面积为S1,满足条件[x2]+[y]2≤1的点(x,y)构成的平面区域的面积为S2,(其中[x]、[y]分别表示不大于x、y的最大整数),则点(S1,S2)一定在( )
| A. | 直线x-y=0上 | B. | 直线2x-y-1=0右下方的区域内 | ||
| C. | 直线x+y-8=0左下方的区域内 | D. | 直线x-y+2=0左上方的区域内 |
7.若函数f(x)=1+$\frac{a}{{a}^{x}-1}$是奇函数,则a的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |