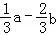题目内容
若a、b是两个非零向量,且|a|=|b|=λ|a+b|,λ∈ ,则b与a-b的夹角的取值范围是 .
,则b与a-b的夹角的取值范围是 .
 ,则b与a-b的夹角的取值范围是 .
,则b与a-b的夹角的取值范围是 .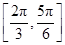
设b与a-b的夹角为θ,
∵λ|a+b|=|b|,|a|=|b|,
∴λ2(a2+2a·b+a2)=a2,
∴a·b=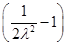 a2,
a2,
又|a-b|2=a2-2a·b+a2
=2a2-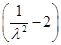 a2
a2
=(4-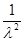 )a2.
)a2.
而cos θ=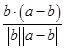
=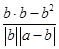
=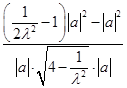
=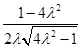
=-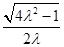
=-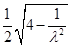 .
.
由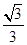 ≤λ≤1得1≤
≤λ≤1得1≤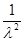 ≤3,
≤3,
∴-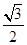 ≤-
≤-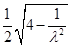 ≤-
≤-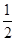 ,
,
∴-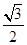 ≤cos θ≤-
≤cos θ≤-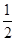 ,
,
∴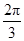 ≤θ≤
≤θ≤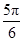 .
.
∵λ|a+b|=|b|,|a|=|b|,
∴λ2(a2+2a·b+a2)=a2,
∴a·b=
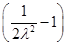 a2,
a2,又|a-b|2=a2-2a·b+a2
=2a2-
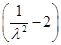 a2
a2=(4-
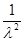 )a2.
)a2.而cos θ=
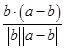
=
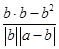
=
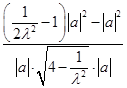
=
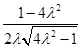
=-
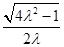
=-
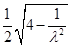 .
.由
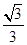 ≤λ≤1得1≤
≤λ≤1得1≤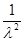 ≤3,
≤3,∴-
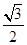 ≤-
≤-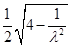 ≤-
≤-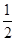 ,
,∴-
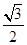 ≤cos θ≤-
≤cos θ≤-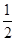 ,
,∴
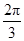 ≤θ≤
≤θ≤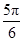 .
.
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 、
、 、
、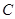 在一条直线上,
在一条直线上,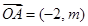 ,
,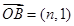 ,
,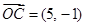 ,且
,且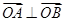 ,其中
,其中 为坐标原点.
为坐标原点.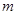 ,
,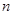 的值;
的值;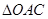 的重心为
的重心为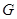 ,若存在实数
,若存在实数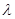 ,使
,使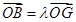 ,试求
,试求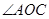 的大小.
的大小.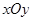 中,
中,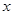 轴方向水平向右,
轴方向水平向右,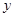 方向指向左上方,且
方向指向左上方,且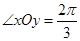 ,平面上任一点
,平面上任一点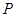 关于斜坐标系的斜坐标是这样定义的:若
关于斜坐标系的斜坐标是这样定义的:若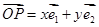 (其中向量
(其中向量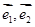 分别是与
分别是与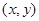 ,那么以
,那么以 为顶点,
为顶点,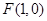 为焦点,
为焦点,


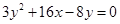
 是非零向量,则
是非零向量,则 是
是 的( )
的( )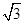 sin x,sin x),b="(cos" x,sin x),x∈
sin x,sin x),b="(cos" x,sin x),x∈ .
. ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ +μ
+μ ,且λμ=
,且λμ= .
.
 |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.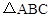 所在的平面内,点
所在的平面内,点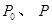 满足
满足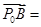
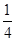
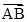 ,
,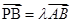 ,且对于任意实数
,且对于任意实数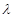 ,恒有
,恒有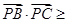
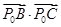 ,则 ( )
,则 ( )



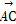 =c,
=c,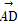 =d,则
=d,则 = (用c与d表示).
= (用c与d表示).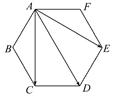
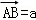 ,
,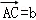 ,则
,则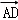 =( )
=( )
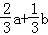 B.
B.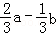 C.
C.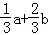 D.
D.