题目内容
在12点时,时针与分针正好重合,那么再经过多少时间,时针与分针再一次重合?在12小时内,两针共重合多少次?
解:设12点时,两针重合的位置为始边,时针转过θ角时,两针重合,则分针转过12θ角,因为两角终边相同,故
12θ=θ+k·360°(k∈Z),所以θ=![]() (k∈Z).
(k∈Z).
又因为时针转过30°时,时间经过1小时,所以时针转过1°时,时间经过![]() 小时,故时针转过θ角经过的时间为
小时,故时针转过θ角经过的时间为![]() k小时.
k小时.
令k=1,得t1=![]() 小时,即时针和分针再一次重合的时间是
小时,即时针和分针再一次重合的时间是![]() 小时.
小时.
又由0°≤θ<360°及θ=![]() ,得0≤k≤11(k∈N*),所以12小时内,两针共重合11次.
,得0≤k≤11(k∈N*),所以12小时内,两针共重合11次.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
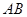 是底部
是底部 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物,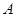 为塔的最高点.现需在对岸测出塔高
为塔的最高点.现需在对岸测出塔高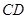 ,使
,使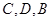 三点不在同一条直线上,测出
三点不在同一条直线上,测出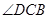 及
及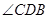 的大小(分别用
的大小(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用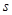 表示测得的数据),另外需在点
表示测得的数据),另外需在点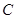 测得塔顶
测得塔顶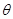 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高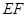 ,使
,使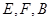 三点在同一条直线上.在
三点在同一条直线上.在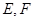 处分别测得塔顶
处分别测得塔顶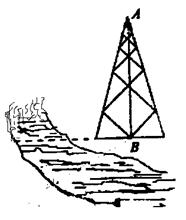
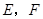 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高