题目内容
设双曲线  的右焦点为
的右焦点为 ,右准线
,右准线  与两条渐近线交于
与两条渐近线交于 两点,如果
两点,如果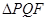 是等边三角形,则双曲线的离心率
是等边三角形,则双曲线的离心率 的值为( )
的值为( )
A. | B. | C.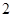 | D. |
C
解析试题分析:双曲线C的右焦点F(c,0),右准线l的方程为:x= ,两条渐近线方程为:y=±
,两条渐近线方程为:y=± .
.
∴两交点坐标为 P( ,
, )、Q(
)、Q( ,-
,- ).
).
设M为PQ与x轴的交点,∵△PFQ为等边三角形,则有|MF|= |PQ|(如图).
|PQ|(如图).
∴c- =
= •(
•( +
+ ),即
),即 .
.
解得 b= a,c=2a.
a,c=2a.
∴e=2,故选C。
考点:本题主要考查双曲线的标准方程及其几何性质,直线与双曲线的位置关系。
点评:典型题,利用数形结合思想,发现a,b,c,e的关系。

练习册系列答案
相关题目
抛物线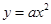 的焦点坐标是( )
的焦点坐标是( )
A. | B.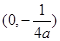 | C. | D. |
方程2x2+ky2=1表示的是焦点在y轴上的椭圆,则实数k的取值范围是( )
| A.(0,+∞) | B.(2,+∞) | C.(0,2) | D.(0,1) |
设抛物线的顶点在原点,焦点与椭圆 的右焦点重合,则此抛物线的方程是( )
的右焦点重合,则此抛物线的方程是( )
| A.y2=-8x | B.y2=-4x | C.y2="8x" | D.y2=4x |
已知椭圆 (
( )中,
)中, 成等比数列,则椭圆的离心率为( )
成等比数列,则椭圆的离心率为( )
A. | B.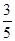 | C. | D. |
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. | B. | C. | D.4 |
过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,点O是坐标原点,则|AF|·|BF|的最小值是( )
| A.2 | B. | C.4 | D.2 |
抛物线 上一点
上一点 到焦点的距离为1,则点
到焦点的距离为1,则点 的纵坐标是 ( )
的纵坐标是 ( )
| A.0 | B. | C. | D. |
 的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且
的焦点为F,A, B是该抛物线上的两点,弦AB过焦点F,且 ,则线段AB的中点坐标是( )
,则线段AB的中点坐标是( )


