题目内容
若定义在R上的函数 对任意的
对任意的 ,都有
,都有
 成立,且当
成立,且当 时,
时, .
.
(1)求 的值;(2)求证:
的值;(2)求证: 是R上的增函数;
是R上的增函数;
(3) 若 ,不等式
,不等式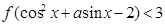 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 对任意的
对任意的 ,都有
,都有 成立,且当
成立,且当 时,
时, .
.(1)求
 的值;(2)求证:
的值;(2)求证: 是R上的增函数;
是R上的增函数;(3) 若
 ,不等式
,不等式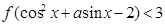 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.(1) (2)略 (3)
(2)略 (3) 
 (2)略 (3)
(2)略 (3) 
本试题主要考查了函数的单调性和不等式的综合运用。
(1)解:定义在R上的函数 对任意的,都有
对任意的,都有 成立
成立
令 ………5分
………5分
(2)证明: 任取 ,且
,且 ,则
,则 ………6分
………6分
 ………7分
………7分
∴ ∴
∴ 是R上的增函数 ………9分
是R上的增函数 ………9分
(3) 解:∵ ,且f(4)=5
,且f(4)=5
∴ f(4)=f(2)+f(2)-1=3 ………10分
由不等式
由(2)知:是R上的增函数
令 则
则 ,
,
故只需 ……12分
……12分
当 即
即 时,
时,  ……13分
……13分
当 即
即 时,
时,
 ………14分
………14分
当 即
即 时,
时,  综上所述, 实数a的取值范围
综上所述, 实数a的取值范围
(1)解:定义在R上的函数
 对任意的,都有
对任意的,都有 成立
成立令
 ………5分
………5分(2)证明: 任取
 ,且
,且 ,则
,则 ………6分
………6分 ………7分
………7分∴
 ∴
∴ 是R上的增函数 ………9分
是R上的增函数 ………9分(3) 解:∵
 ,且f(4)=5
,且f(4)=5∴ f(4)=f(2)+f(2)-1=3 ………10分
由不等式

由(2)知:是R上的增函数

令
 则
则 ,
,故只需
 ……12分
……12分当
 即
即 时,
时,  ……13分
……13分当
 即
即 时,
时,  ………14分
………14分当
 即
即 时,
时,  综上所述, 实数a的取值范围
综上所述, 实数a的取值范围

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
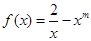 ,且
,且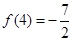 .
.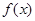 在
在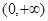 上的单调性,并给予证明;
上的单调性,并给予证明;
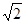 是函数
是函数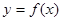 的极值点,其中
的极值点,其中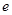 是自然对数的底数.
是自然对数的底数.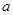 的值;
的值;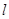 同时满足:
同时满足: 处的切线,
处的切线,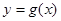 的图象相切于点
的图象相切于点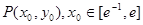 .
. 设
设 是集合P到集合Q的映射,如果Q
是集合P到集合Q的映射,如果Q 则
则 =( )。
=( )。




 .
. 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,求
,求 的值;
的值; 上不单调,求
上不单调,求 的取值范围.
的取值范围. 上的偶函数
上的偶函数 在[—1,0]上是增函数,给出下列关于
在[—1,0]上是增函数,给出下列关于 的判断:
的判断: 对称;
对称; .
. 吨,应交水费
吨,应交水费 元。
元。 ,共交水费26.4元,分别求出甲、乙两用户该月的用水量和水费。
,共交水费26.4元,分别求出甲、乙两用户该月的用水量和水费。 ,其中
,其中 为实数,
为实数, ,
, ,
, ,若
,若 ,则
,则 ;
;