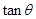题目内容
已知向量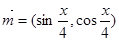 ,
,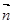 =(
=(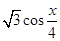 ,
, ),记
),记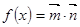 ;
;
(1)若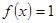 ,求
,求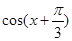 的值;
的值;
(2)若 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.
(1) (2)(1,
(2)(1, )
)
解析试题分析:(1)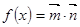 =
= =
= =
= ,
,
∵f(x)=1, ∴ , (4分)
, (4分)
∴ =
= . (6分)
. (6分)
(2)∵(2a-c)cosB=bcosC,∴由正弦定理得 ,
,
∴ ,∴
,∴ ,
,
∵ ,∴
,∴ ,且
,且 ,
,
∴ ∴
∴ ; (10分)
; (10分)
∴ , ∴
, ∴ ∴
∴  ;
;
又∵f(x)= ,∴f(A)=
,∴f(A)= ,
,
故函数f(A)的取值范围是(1, ). (12分)
). (12分)
考点:三角函数化简求值函数性质及解三角形
点评:三角函数化简时主要应用三角函数诱导公式,二倍角公式及关系式 ,解三角形求边角及关系式时常借助于正余弦定理,第二问在求
,解三角形求边角及关系式时常借助于正余弦定理,第二问在求 范围的时候需结合三角函数图像及单调区间考虑
范围的时候需结合三角函数图像及单调区间考虑

练习册系列答案
相关题目
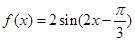
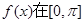 内的单调递增区间;
内的单调递增区间;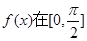 内的值域.
内的值域.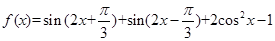 ,
, .
. 求函数
求函数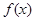 的最小正周期;
的最小正周期; 若函数
若函数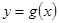 的图像和
的图像和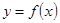 的图像关于直线
的图像关于直线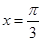 对称,求
对称,求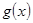 在
在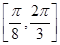 上的最大值和最小值.
上的最大值和最小值.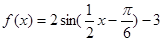 ,
,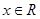 .
. 的最小正周期及对称中心;
的最小正周期及对称中心; 的最大值为M,最小正周期为T。
的最大值为M,最小正周期为T。

 的图象经过点
的图象经过点 ,
, ,当
,当 时,恒有
时,恒有 ,求实数
,求实数 的取值范围。
的取值范围。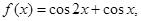
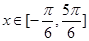 ,求函数
,求函数 的值域.
的值域.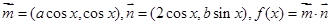 且
且
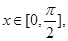 ,求
,求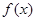 的最大值与最小值
的最大值与最小值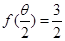 ,且
,且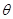 是三角形的一个内角,求
是三角形的一个内角,求