题目内容
4．已知实数x、y满足|2x+3y|＜$\frac{1}{3}$，|x-2y|＜$\frac{1}{6}$，求证：|y|＜$\frac{2}{21}$．分析 通过去绝对值符号可知-$\frac{1}{3}$＜2x+3y＜$\frac{1}{3}$、-$\frac{1}{6}$＜2y-x＜$\frac{1}{6}$即-$\frac{1}{3}$＜4y-2x＜$\frac{1}{3}$，两式相加、计算即得结论．
解答 证明：∵|2x+3y|＜$\frac{1}{3}$，
∴-$\frac{1}{3}$＜2x+3y＜$\frac{1}{3}$，①
∵|x-2y|＜$\frac{1}{6}$，
∴-$\frac{1}{6}$＜2y-x＜$\frac{1}{6}$，
∴-$\frac{1}{3}$＜4y-2x＜$\frac{1}{3}$，②
由①、②可知-$\frac{2}{3}$＜7y＜$\frac{2}{3}$，
∴-$\frac{2}{21}$＜y＜$\frac{2}{21}$，即|y|＜$\frac{2}{21}$．
点评 本题考查不等式的证明，去绝对值符号、利用不等式的性质是解决本题的关键，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
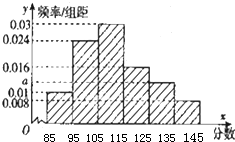某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示，全市10000名学生的成绩服从正态分布N （120，25），现某校随机抽取了50名学生的数学成绩分析，结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组，第一组[85，95），第二组[95，105），…第六组[135，145]，得到如图所示的频率分布直方图．
9．已知f（x）是定义在R上的偶函数且在[0，+∞）上递增，p：f（$\frac{x}{x+1}$）＜f（-$\frac{1}{2}$），q：|x-a|＜1，若p是q的充分不必要条件，则实数a的取值范围为（ ）
| A． | （0，$\frac{4}{3}$） | B． | （-∞，0）∪（$\frac{4}{3}$，+∞） | C． | （-∞，0]∪[$\frac{4}{3}$，+∞） | D． | [0，$\frac{2}{3}$] |