题目内容
已知f(x)=-logcosφ(x2-ax+3a)(φ为锐角),在区间[2,+∞)上为增函数,则实数a的取值范围是________.
-4<a≤4
分析:将原函数看作是复合函数,令u=x2-ax+3a,且g(x)>0,因为函数是二次函数,所以用二次函数的图象与性质来判断其单调性,再由复合函数“同增异减”求得结果.
解答:令u=x2-ax+3a,
∵0<cosφ<1,
∴y=logcosφu在定义域内为减函数,
∴f(x)=-logcosφ(x2-ax+3a)在[2,+∞)上为增函数,
则u=x2-ax+3a>0在[2,+∞)上恒成立,且为增函数,
∴ ,
,
解得-4<a≤4.
故答案为:-4<a≤4.
点评:本题主要考查复合函数的单调性,结论是同增异减,解题时一定要注意定义域.
分析:将原函数看作是复合函数,令u=x2-ax+3a,且g(x)>0,因为函数是二次函数,所以用二次函数的图象与性质来判断其单调性,再由复合函数“同增异减”求得结果.
解答:令u=x2-ax+3a,
∵0<cosφ<1,
∴y=logcosφu在定义域内为减函数,
∴f(x)=-logcosφ(x2-ax+3a)在[2,+∞)上为增函数,
则u=x2-ax+3a>0在[2,+∞)上恒成立,且为增函数,
∴
 ,
,解得-4<a≤4.
故答案为:-4<a≤4.
点评:本题主要考查复合函数的单调性,结论是同增异减,解题时一定要注意定义域.

练习册系列答案
相关题目
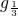 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间. [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.