题目内容
已知f(x)=lo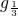 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.
解:∵真数3-(x-1)2≤3,
∴lo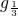 [3-(x-1)2]≥log
[3-(x-1)2]≥log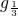 3=-1,即f(x)的值域是[-1,+∞).
3=-1,即f(x)的值域是[-1,+∞).
又3-(x-1)2>0,得1- <x<1+
<x<1+ ,
,
∴x∈(1- ,1]时,3-(x-1)2单调递增,从而f(x)单调递减;
,1]时,3-(x-1)2单调递增,从而f(x)单调递减;
x∈[1,1+ )时,f(x)单调递增.
)时,f(x)单调递增.
所以,f(x)的值域是[-1,+∞).
f(x)单调递减区间:(1- ,1]
,1]
f(x)单调递增区间:[1,1+ )
)
分析:确定真数的范围,利用对数函数的性质,直接推出函数的值域;再求出对数的真数大于0时的对称轴,利用复合函数的单调性求出单调区间.
点评:本题考查对数函数的单调区间,对数函数的值域与最值,是中档题.
∴lo
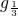 [3-(x-1)2]≥log
[3-(x-1)2]≥log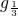 3=-1,即f(x)的值域是[-1,+∞).
3=-1,即f(x)的值域是[-1,+∞).又3-(x-1)2>0,得1-
 <x<1+
<x<1+ ,
,∴x∈(1-
 ,1]时,3-(x-1)2单调递增,从而f(x)单调递减;
,1]时,3-(x-1)2单调递增,从而f(x)单调递减;x∈[1,1+
 )时,f(x)单调递增.
)时,f(x)单调递增.所以,f(x)的值域是[-1,+∞).
f(x)单调递减区间:(1-
 ,1]
,1]f(x)单调递增区间:[1,1+
 )
)分析:确定真数的范围,利用对数函数的性质,直接推出函数的值域;再求出对数的真数大于0时的对称轴,利用复合函数的单调性求出单调区间.
点评:本题考查对数函数的单调区间,对数函数的值域与最值,是中档题.

练习册系列答案
相关题目
 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.