题目内容
将等差数列3, 6, 9, 12, 15, 18, 21, …3n, …① 各项依次分组得数列: 3,(6+9), (12+15+18), (21+24+27+30), …②,这里第一项含1个数, 第二项含2个数, 第三项含3个数, …, 则数列②的第n项是[ ]
A.![]() (n+1) B.
(n+1) B.![]() (n2+1)
C.
(n2+1)
C.![]() (n-1) D.
(n-1) D.![]() (n2-1)
(n2-1)
答案:B
解析:
提示:
解析:
|
解: ∵数列①的通项公式是an=3n, 是公差为3的等差数列. 数列②的第n项是数列①的
∴bn=3( = = |
提示:
| 第二个数列的每一项都是等差数列的和. |

练习册系列答案
相关题目
将连续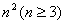 个正整数填入
个正整数填入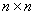 的方格中,使其每行、每列、每条对角线上的各数
的方格中,使其每行、每列、每条对角线上的各数
|
8 |
3 |
4 |
|
1 |
5 |
9 |
|
6 |
7 |
2 |
之和都相等,这个正方形叫做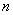 阶幻方数阵,记
阶幻方数阵,记 为
为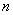 阶幻方数阵对角线上
阶幻方数阵对角线上
各数之和,如图就是一个3阶幻方数阵,可知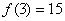 。若将等差数列3,4,5,6,
。若将等差数列3,4,5,6, 的前16 项填入
的前16 项填入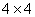 方格中,可得到一个4阶幻方数阵,则
方格中,可得到一个4阶幻方数阵,则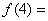 ( )
( )
A.44 B.42 C.40 D.36
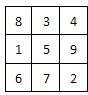 将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于
将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于