题目内容
9.已知{an}是递增的等差数列a3=$\frac{5}{2}$,且a2a4=6.(1)求{an}的首项a1和公差d;
(2)求{an}的通项和前n项和Sn.
分析 (1)由题意得公差d>0,运用等差数列中项的性质,解方程可得a2=2,a4=3,运用等差数列的通项公式可得公差d和首项;
(2)运用等差数列的通项公式和求和公式,化简计算即可得到所求.
解答 解:(1)由题意得公差d>0,
a3=$\frac{5}{2}$,且a2a4=6,
可得a2+a4=2a3=5,
解得a2=2,a4=3,
可得2d=a4-a2=1,解得d=$\frac{1}{2}$,
则a1=a2-d=$\frac{3}{2}$;
(2){an}的通项an=a1+(n-1)d=$\frac{3}{2}$+$\frac{1}{2}$(n-1)=$\frac{1}{2}$(n+2);
前n项和Sn=na1+$\frac{1}{2}$n(n-1)d=$\frac{3}{2}$n+$\frac{1}{4}$n(n-1)=$\frac{1}{4}$n2+$\frac{5}{4}$n.
点评 本题考查等差数列的通项公式和求和公式的运用,以及等差数列的性质,运用方程思想和公式法是解题的关键,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.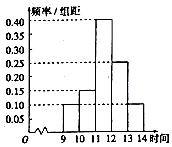 一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
 一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )| A. | 100万元 | B. | 10万元 | C. | 7.5万元 | D. | 6.25万元 |