题目内容

已知等腰梯形PDCB中，PB=3，DC=1，PD=
2
，A为PB边上一点，且DA⊥PB，将△PAD沿AD折起，使PA⊥AB．
（1）求证：CD∥面PAB；
（2）求证：CB⊥面PAC．
精英家教网
证明：（1）∵四边形PDCB为梯形
∴CD∥AB
由于对折后CD?面PAB，且AB?面PAB
∴CD∥面PAB；
（2）在等腰梯形PDCB中，
∵PB=3，DC=1，PD=
2
，
∴AC=BC=
2
，AB=2
由勾股定理可得BC⊥AC
又∵PA⊥AB，PA⊥AD，AB∩AD=A
∴PA⊥平面ABD
又∵BC?平面ABD
∴BC⊥PA，
又PA∩AC=A，
∴CB⊥面PAC
练习册系列答案
相关题目
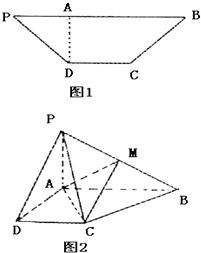精英家教网已知等腰梯形PDCB中（如图1），PB=3，DC=1，PB=BC=2a=|
QP
|+|
QP′
|=
(
5
2
-2)2+(
3
2
)2
+
(
5
2
+2)2+(
3
2
)2
=2
10
，A为PB边上一点，且PA=1，将△PAD沿AD折起，使面PAD⊥面ABCD（如图2）
（I）证明：平面PAD⊥PCD；
（II）试在棱PB上确定一点M，使截面AMC把几何体分成的两部分VPDCMA：VMACB=2：1；
（III）在M满足（Ⅱ）的情况下，判断直线AM是否平行面PCD．
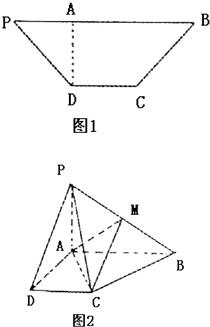精英家教网已知等腰梯形PDCB中（如图1），PB=3，DC=1，PD=BC=
2
，A为PB边上一点，且PA=1，将△PAD沿AD折起，使面PAD⊥面ABCD（如图2）．
（1）证明：平面PAD⊥平面PCD；
（2）试在棱PB上确定一点M，使截面AMC把几何体分成的两部分VPDCMA：VMABC=2：1．
（3）在M满足（Ⅱ）的情况下，判断直线AM是否平行面PCD．
已知等腰梯形PDCB中，PB=3，DC=1，PD=
2
，A为PB边上一点，且DA⊥PB，将△PAD沿AD折起，使PA⊥AB．
（1）求证：CD∥面PAB；
（2）求证：CB⊥面PAC．
（2008•盐城一模）已知等腰梯形PDCB中，PB=3，DC=1，PD=BC=
2
，A为PB边上一点，且PA=1，将△PAD沿AD折起，使面PAD⊥面ABCD．
（Ⅰ）证明：平面PAD⊥平面PCD；
（Ⅱ）试在棱PB上确定一点M，使截面AMC把几何体分成的两部分VP-DCMA：VM-ACB=2：1．

 

（09年莱西一中模拟理）（12分）

已知等腰梯形PDCB中（如图1），PB=3，DC=1，PD=BC=，A为PB边上一点，且PA=1，将△PAD沿AD折起，使面

PAD⊥面ABCD（如图2）。

   （Ⅰ）证明：平面PAD⊥PCD；

   （Ⅱ）试在棱PB上确定一点M，使截面AMC把几何体分成的两部分；

   （Ⅲ）在M满足（Ⅱ）的情况下，判断直线AM是否平行面PCD.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网