Question

 

（09年莱西一中模拟理）（12分）

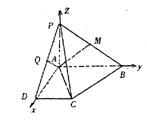
已知等腰梯形PDCB中（如图1），PB=3，DC=1，PD=BC=，A为PB边上一点，且PA=1，将△PAD沿AD折起，使面

PAD⊥面ABCD（如图2）。

   （Ⅰ）证明：平面PAD⊥PCD；

   （Ⅱ）试在棱PB上确定一点M，使截面AMC把几何体分成的两部分；

   （Ⅲ）在M满足（Ⅱ）的情况下，判断直线AM是否平行面PCD.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Answer 1

 解析：（I）证明：依题意知：

                      …………2分

   …4分

   （II）由（I）知平面ABCD

    ∴平面PAB⊥平面ABCD.               …………4分

   在PB上取一点M，作MN⊥AB，则MN⊥平面ABCD，

    设MN=h

    则

                …………6分

    要使

    即M为PB的中点.                                      …………8分

   （III）以A为原点，AD、AB、AP所在直线为x，y，z轴，

    建立如图所示的空间直角坐标系

   

则A（0，0，0），B（0，2，0），

    C（1，1，0），D（1，0，0），

    P（0，0，1），M（0，1，）

    由（I）知平面，则

    的法向量。           …………10分

    又为等腰

   

    因为

所以AM与平面PCD不平行.    …………12分