题目内容
函数y=1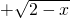
的定义域是________．
{x|x≤2}
分析：由2-x≥0求解x的取值集合即可得到原函数的定义域．
解答：由2-x≥0，得x≤2．
所以原函数的定义域为{x|x≤2}．
故答案为{x|x≤2}．
点评：本题考查了函数的定义域及其求法，函数的定义域就是使函数解析式有意义的自变量的取值范围，是基础题．
分析：由2-x≥0求解x的取值集合即可得到原函数的定义域．
解答：由2-x≥0，得x≤2．
所以原函数的定义域为{x|x≤2}．
故答案为{x|x≤2}．
点评：本题考查了函数的定义域及其求法，函数的定义域就是使函数解析式有意义的自变量的取值范围，是基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
函数y=
的定义域是（ ）
| log2x |
| A、（0，1] |
| B、（0，+∞） |
| C、[1，+∞） |
| D、（1，+∞） |
设a∈{-1，1，
，3}，则使函数y=xa的定义域是R，且为奇函数的所有a的值是（ ）
| 1 |
| 2 |
| A、1，3 | B、-1，1 |
| C、-1，3 | D、-1，1，3 |
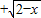的定义域是 ．