题目内容
(本小题满分12分)已知椭圆与双曲线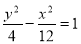 的焦点相同,且它们的离心率之和等于
的焦点相同,且它们的离心率之和等于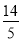 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)过椭圆内一点 作一条弦
作一条弦 ,使该弦被点
,使该弦被点 平分,求弦
平分,求弦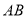 所在直线方程.
所在直线方程.
(Ⅰ)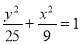
(Ⅱ)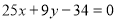
【解析】
试题分析:对于第一问,根据所给的双曲线的方程,可以得出焦点坐标,对应的离心率,所以可以求得所求的椭圆的离心率,从而得出对应的椭圆的a,进而求得椭圆的方程,对于第二问,涉及到椭圆的中点弦所在直线的方程问题,注意可以先将直线的斜率设出来,联立方程组,根据中点的坐标可以求得两根和,从而求k的值,也可以应用点差法求得斜率,应用点斜式方程直接得结果.
试题解析:(Ⅰ)由题意知,双曲线的焦点坐标为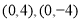 ,离心率为
,离心率为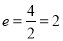 , 2分
, 2分
设椭圆方程: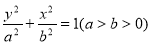 ,则
,则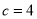
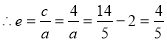 ,
,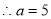 , 4分
, 4分
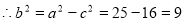 , 5分
, 5分
 椭圆方程为:
椭圆方程为: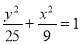 . 6分
. 6分
(Ⅱ)解法一:设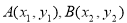 ,
,
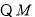 为弦
为弦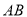 的中点,
的中点,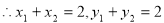 , 7分
, 7分
由题意: ,
,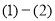 得
得
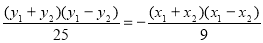 ,
,
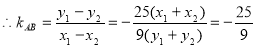 , 10分
, 10分
此时直线方程为: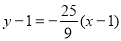 ,即
,即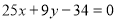 ,
,
故所求弦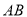 所在的直线方程为
所在的直线方程为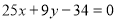 . 12分
. 12分
解法二:由题意可知,直线斜率必存在.设所求直线方程为: ,
,
由 ,得
,得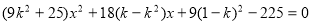 ,(*) 8分
,(*) 8分
设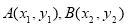 ,
, 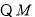 为弦
为弦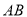 的中点,
的中点,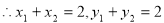 ,
,
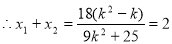 ,
,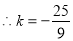 , 10分
, 10分
故所求弦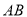 所在的直线方程为:
所在的直线方程为: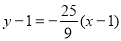 ,即
,即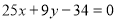 . 12分
. 12分
考点:椭圆的方程,椭圆的中点弦所在直线的方程.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 考点3:双曲线的标准方程 考点4:双曲线的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
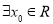 ,使得
,使得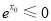
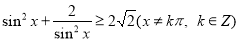

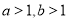 是
是 的充分不必要条件
的充分不必要条件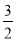 B.0 C.1 D.0或-
B.0 C.1 D.0或-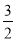
 中,
中, ,则数列
,则数列 是等比数列,命题
是等比数列,命题 “若公比
“若公比 ,则数列
,则数列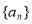 是首项为
是首项为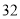 的等比数列,
的等比数列,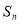 是其前
是其前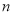 项和,且
项和,且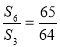 ,则数列
,则数列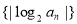 前
前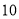 项和为 ( )
项和为 ( ) 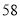 B.
B.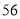 C.
C.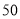 D.
D.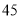
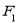 ,右焦点为
,右焦点为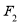 .若椭圆上存在一点
.若椭圆上存在一点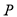 ,满足线段
,满足线段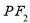 相切于以椭圆的短轴为直径的圆,切点为线段
相切于以椭圆的短轴为直径的圆,切点为线段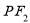 的中点,则该椭圆的离心率为 ( )
的中点,则该椭圆的离心率为 ( )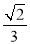 B.
B.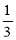 C.
C.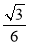 D.
D.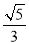
 上的点,若过点P的切线方程与直线
上的点,若过点P的切线方程与直线 垂直,则过P点处的切线方程是____________.
垂直,则过P点处的切线方程是____________.