题目内容
(本题满分14分)在△ABC中,角A、B、C的所对边的长分别为a、b、c,且a=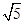 ,b=3,sinC=2sinA.
,b=3,sinC=2sinA.
(Ⅰ)求c的值;
(Ⅱ)求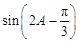 的值.
的值.
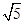 ,b=3,sinC=2sinA.
,b=3,sinC=2sinA.(Ⅰ)求c的值;
(Ⅱ)求
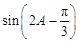 的值.
的值.解:(Ⅰ)根据正弦定理,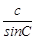 =
=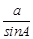 ,所以c=
,所以c=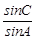 a=2a=2
a=2a=2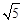 .(5分)
.(5分)
(Ⅱ)根据余弦定理,得cosA=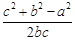 =
=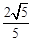 ,
,
于是sinA=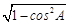 =
=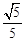 ,
,
从而sin2A=2sinAcosA=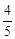 ,
,
cos2A=cos2A-sin2A=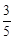 ,
,
所以sin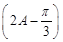 =sin2Acos
=sin2Acos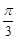 -cos2Asin
-cos2Asin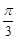 =
=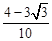 .(14分)
.(14分)
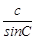 =
=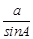 ,所以c=
,所以c=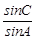 a=2a=2
a=2a=2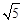 .(5分)
.(5分)(Ⅱ)根据余弦定理,得cosA=
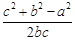 =
=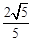 ,
,于是sinA=
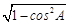 =
=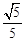 ,
,从而sin2A=2sinAcosA=
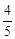 ,
,cos2A=cos2A-sin2A=
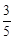 ,
,所以sin
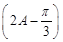 =sin2Acos
=sin2Acos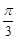 -cos2Asin
-cos2Asin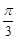 =
=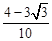 .(14分)
.(14分)略

练习册系列答案
相关题目
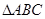 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为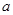 、
、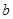 、
、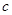 ,已知
,已知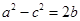 ,且
,且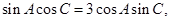 则b=____________.
则b=____________.
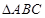 中,
中,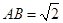 ,
,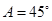 ,
,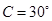 ,则
,则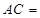
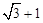
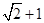
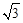
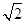
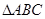 中,角
中,角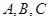 所对的边分别为
所对的边分别为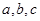 ,已知
,已知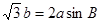

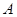 的大小;(2)若
的大小;(2)若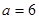 ,求
,求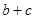 的取值范围.
的取值范围. 中,
中,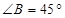 ,
, ,则
,则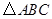 中,
中,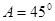 ,
,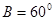 ,
,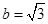 ,那么
,那么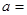
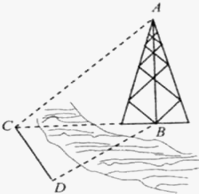
 中,若
中,若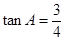 ,
, ,
,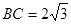 ,则
,则 。
。