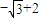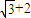题目内容
设函数f(x)为偶函数,且当x∈[0,2)时,f(x)=2sinx,当x∈[2,+∞)时f(x)=log2x,则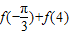 =( )
=( )A.
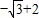
B.3
C.
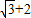
【答案】分析:函数f(x)为偶函数,可得f(- )=f(
)=f( )再将其代入f(x)=2sinx,进行求解,再根据x∈[2,+∞)时f(x)=log2x,求出f(4),从而进行求解;
)再将其代入f(x)=2sinx,进行求解,再根据x∈[2,+∞)时f(x)=log2x,求出f(4),从而进行求解;
解答:解:∵函数f(x)为偶函数,
∴f(- )=f(
)=f( ),
),
∵当x∈[0,2)时f(x)=2sinx,
∴f(x)=2sin =2×
=2× =
= ;
;
∵当x∈[2,+∞)时f(x)=log2x,
∴f(4)=log24=2,
∴ =
= +2,
+2,
故选C;
点评:此题主要考查函数值的求解问题,解题的过程中需要注意函数的定义域,是一道基础题;
 )=f(
)=f( )再将其代入f(x)=2sinx,进行求解,再根据x∈[2,+∞)时f(x)=log2x,求出f(4),从而进行求解;
)再将其代入f(x)=2sinx,进行求解,再根据x∈[2,+∞)时f(x)=log2x,求出f(4),从而进行求解;解答:解:∵函数f(x)为偶函数,
∴f(-
 )=f(
)=f( ),
),∵当x∈[0,2)时f(x)=2sinx,
∴f(x)=2sin
 =2×
=2× =
= ;
;∵当x∈[2,+∞)时f(x)=log2x,
∴f(4)=log24=2,
∴
 =
= +2,
+2,故选C;
点评:此题主要考查函数值的求解问题,解题的过程中需要注意函数的定义域,是一道基础题;

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
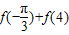 =( )
=( )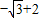
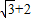
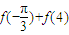 =( )
=( )