题目内容
(本小题满分13分)从甲、乙两班某项测试成绩中各随机抽取5名同学的成绩,得到如下茎叶图.已知甲班样本成绩的中位数为13, 乙班样本成绩的平均数为16.

(1)求 的值;
的值;
(2)试估计甲、乙两班在该项测试中整体水平的高低(只需写出结论);
(3)从两组样本成绩中分别去掉一个最低分和一个最高分,再从两组
剩余成绩中分别随机选取一个成绩,求这两个成绩的和 的分布列及数学期望.
的分布列及数学期望.
(注:方差 ,其中
,其中 为
为 ,
, , ,
, , 的平均数.)
的平均数.)
(1) ,
, ; (2)乙班的水平高;(3)详见解析.
; (2)乙班的水平高;(3)详见解析.
【解析】
试题分析:(1)利用平均数的公式列方程分别求 的值,利用中位数的概念求
的值,利用中位数的概念求 ;
;
(2)通过比较两组数据的平均值和方差来分析两组整体水平的高低;
(3)根据(1)的结果,从甲、乙两班测试中分别去掉一个最低分和最高分,则甲班:12,13,20,乙班:15,18,18.剩余成绩中分别随机选取一个成绩,共有九个不同结果,每个结果发生的概率均为 ,但两个成绩的和
,但两个成绩的和 有27,28,30,31,35,38六个可能的取值,利用古典概型求出
有27,28,30,31,35,38六个可能的取值,利用古典概型求出 取每个可能值的概率,从而得到
取每个可能值的概率,从而得到 的分布列及数学期望.
的分布列及数学期望.
试题解析:【解析】
(1)经计算得:甲班数据依次为 ,所以中位数为
,所以中位数为 ,得
,得 ;
; ,得
,得 . 4分
. 4分
(2)乙班整体水平高.
或【解析】
 ,
,
 ,
,
 ,
,
 .
.
因为 ,所以乙班的水平高. 7分
,所以乙班的水平高. 7分
(3)从甲、乙两班测试中分别去掉一个最低分和最高分,则甲班:12,13,20,
乙班:15,18,18.
这两班测试成绩的和为 ,则
,则 ,
,
所以 ,
, ,
, ,
, ,
, ,
, .
.
所以 的分布列为
的分布列为
| 27 | 28 | 30 | 31 | 35 | 38 |
|
|
|
|
|
|
|
所以 的期望为
的期望为

 13分
13分
考点:1、茎叶图;2、平均数和中位数的概念;3、离散型随机变量的分布列与数学期望.

练习册系列答案
相关题目




 中,角
中,角 的对边分别是
的对边分别是 ,
,  的面积为
的面积为 ,则
,则 ;
; .
. 的图形的一条对称轴经过点( ) .
的图形的一条对称轴经过点( ) .



 满足
满足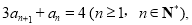 且
且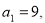 其前
其前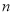 项之和为
项之和为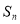 ,则满足不等式
,则满足不等式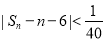 成立的
成立的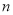 的最小值是
的最小值是 则
则 等于
等于 B.
B. C.
C. D.
D.
 ,
, 满足约束条件
满足约束条件 则
则 的最大值是 .
的最大值是 .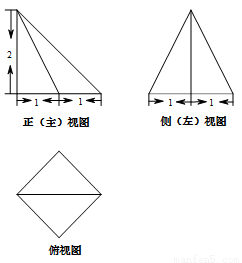
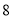 B.
B. C.
C.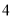 D.
D.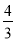
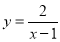 的定义域是(-∞,1)∪[2,5),则其值域是( )
的定义域是(-∞,1)∪[2,5),则其值域是( ) 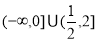 B.(-∞,2]
B.(-∞,2]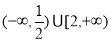 D.(0,+∞)
D.(0,+∞) 的方程为
的方程为 ,圆
,圆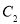 的方程
的方程 ,过
,过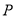 作圆
作圆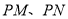 ,切点分别为
,切点分别为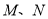 ,则
,则 的最大值为
的最大值为 B.
B. C.
C. D.
D.