题目内容
设椭圆C: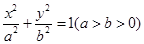 的两个焦点为F1、F2,点B1为其短轴的一个端点,满足
的两个焦点为F1、F2,点B1为其短轴的一个端点,满足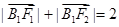 ,
,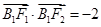 。
。
(1)求椭圆C的方程;
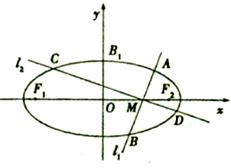
(2)过点M 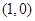 做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。
做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。
(1) (2)
(2)
解析试题分析:解:(Ⅰ)不妨设




所以椭圆方程为
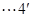
(Ⅱ)①当直线 与
与 轴重合时,
轴重合时,
设 ,则
,则

②当直线 不与
不与 轴重合时,设其方程为
轴重合时,设其方程为 ,设
,设
由 得
得

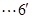




由 与
与 垂直知:
垂直知:



当且仅当 取到“=”.
取到“=”.
综合①②,


考点:椭圆的方程,直线与椭圆的位置关系
点评:解决的关键是利用直线与椭圆的方程联立方程组,结合韦达定理以及向量的数量积公式得到关系式,结合不等式加以证明,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
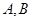 是椭圆
是椭圆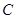 :
: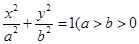 且
且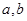 为常数
为常数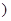 上关于原点对称的两点,点
上关于原点对称的两点,点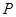 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线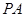 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为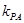 ,
,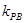 ,那么
,那么 .
.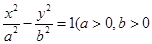 且
且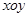 中,曲线
中,曲线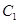 的参数方程为
的参数方程为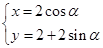 (
(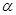 为参数)
为参数)  是
是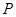 点满足
点满足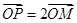 ,
,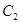 .
. 为极点,
为极点,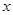 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线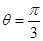 与
与 ,与
,与 ,求
,求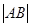 .
. 的直线
的直线 交直线
交直线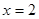 于
于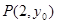 ,过点
,过点 的直线
的直线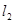 交
交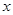 轴于
轴于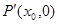 点,
点,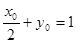 ,
,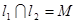 .
.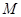 的轨迹
的轨迹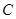 的方程;
的方程;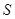 、
、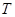 ,已知点
,已知点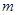 )在线段
)在线段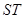 的垂直平分线上且
的垂直平分线上且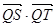 ≤4,求实数
≤4,求实数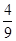 ,求顶点A的轨迹方程.?
,求顶点A的轨迹方程.? 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为 .
.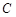 的标准方程;
的标准方程;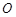 的直线
的直线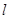 与椭圆
与椭圆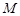 、
、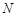 ,且直线
,且直线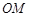 、
、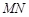 、
、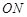 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△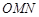 面积的取值范围.
面积的取值范围.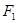 、
、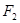 分别为椭圆
分别为椭圆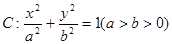 的左、右两个焦点.
的左、右两个焦点.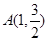 到
到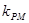 、
、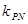 时, 求证:
时, 求证:  O
O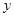 中,直线
中,直线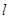 与抛物线
与抛物线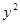 =2
=2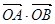 =3”是真命题;
=3”是真命题;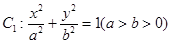 的右焦点
的右焦点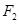 与抛物线
与抛物线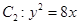 的焦点重合,左端点为
的焦点重合,左端点为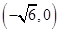
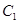 的右焦点且斜率为
的右焦点且斜率为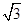 的直线
的直线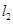 被椭圆
被椭圆 。
。