题目内容
在直角坐标系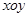 中,曲线
中,曲线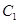 的参数方程为
的参数方程为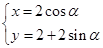 (
(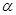 为参数)
为参数)  是
是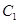 上的动点,
上的动点,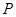 点满足
点满足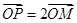 ,
,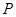 点的轨迹为曲线
点的轨迹为曲线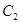 .
.
(1)求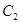 的方程;
的方程;
(2)在以 为极点,
为极点,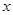 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线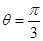 与
与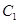 的异于极点的交点为
的异于极点的交点为 ,与
,与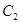 的异于极点的交点为
的异于极点的交点为 ,求
,求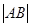 .
.
(1) 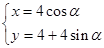 (α为参数) ; (2) |AB|=|ρ2-ρ1|=2
(α为参数) ; (2) |AB|=|ρ2-ρ1|=2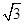 .
.
解析试题分析:(1)设P(x,y),则由条件知M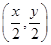 ,
,
由于M点在C1上,所以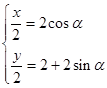
从而C2的参数方程为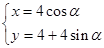 (α为参数) 5分
(α为参数) 5分
(2)曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ.
射线θ=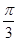 与C1的交点A的极径为ρ1=4sin
与C1的交点A的极径为ρ1=4sin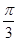 ,
,
射线θ=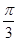 与C2的交点B的极径为ρ2=8sin
与C2的交点B的极径为ρ2=8sin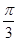 .
.
所以|AB|=|ρ2-ρ1|=2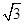 . 10分
. 10分
考点:本题主要考查平面向量的线性运算,极坐标的应用,参数方程的求法,直线与圆的位置关系。
点评:中档题,确定参数方程的过程中, 利用了“代入法”。利用极坐标方程,确定线段的长度,令人耳目一新。

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 和
和 ,且|
,且| )在该椭圆上.
)在该椭圆上.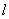 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A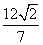 ,求以
,求以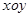 中,直线
中,直线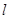 的参数方程为
的参数方程为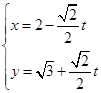 (t 为参数)。在极坐标系(与直角坐标系
(t 为参数)。在极坐标系(与直角坐标系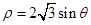 。
。 ),求|PA|+|PB|.
),求|PA|+|PB|. =2x于M(x
=2x于M(x ,y
,y ,y
,y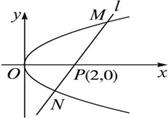
 过点
过点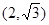 ,且它的离心率
,且它的离心率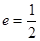 .直线
.直线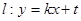 与椭圆
与椭圆 交于
交于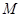 、
、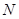 两点.
两点.
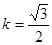 时,求证:
时,求证: 与圆
与圆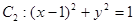 相切,椭圆上一点
相切,椭圆上一点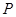 满足
满足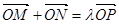 ,求实数
,求实数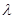 的取值范围.
的取值范围.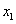 ,
,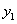 ),B(
),B(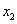 ,
,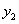 )是函数
)是函数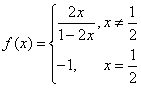 的图象上的任意两点(可以重合),点M在直线
的图象上的任意两点(可以重合),点M在直线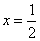 上,且
上,且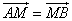 .
.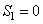 ,当
,当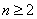 时,
时,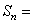
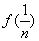 +
+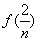 +
+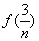 +
+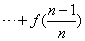 ,求
,求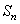 ;
;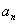 =
=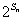 ,
,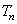 为数列{
为数列{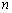 项和,若存在正整数
项和,若存在正整数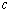 、
、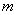 ,
,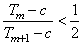 成立,求
成立,求 .
.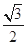 ,求椭圆的标准方程;
,求椭圆的标准方程;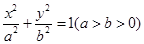 的两个焦点为F1、F2,点B1为其短轴的一个端点,满足
的两个焦点为F1、F2,点B1为其短轴的一个端点,满足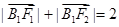 ,
,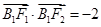 。
。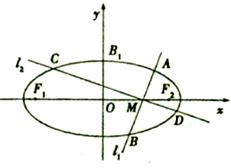
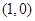 做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。
做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。 轴,且实轴长为2,离心率
轴,且实轴长为2,离心率 , L是过定点
, L是过定点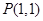 的直线.
的直线.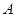 ,
,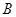 两点,且线段
两点,且线段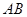 恰好以点
恰好以点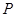 为中点,若存在,求出直线L的方程,若不存,说明理由.
为中点,若存在,求出直线L的方程,若不存,说明理由.