题目内容
已知二次函数 的图象与x轴有两个不同的公共点,且
的图象与x轴有两个不同的公共点,且 ,当
,当 时,恒有
时,恒有 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8,且 ,求a的值;
,求a的值;
(3)若 ,且
,且 对所有
对所有 恒成立,求正实数m的最小值.
恒成立,求正实数m的最小值.
【答案】
(1)当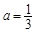 ,c=2时,
,c=2时,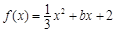 ,f(x)的图像与x轴有两个不同交点,
,f(x)的图像与x轴有两个不同交点,
因为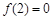 ,设另一个根为x1,则2x1=6,x1=3.
…………2分
,设另一个根为x1,则2x1=6,x1=3.
…………2分
则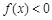 的解集为
的解集为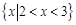 .
…………4分
.
…………4分
(2) 函数f(x)的图像与x轴有两个交点,因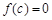 ,
,
设另一个根为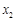 ,则
,则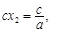 于是
于是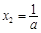 .
…………6分
.
…………6分
又当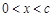 时,恒有
时,恒有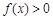 ,则
,则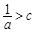 ,则三交点为
,则三交点为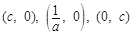 ,8分
,8分
这三交点为顶点的三角形的面积为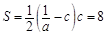 , 且
, 且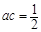 ,
,
解得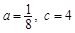 .
………10分
.
………10分
(3)当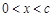 时,恒有
时,恒有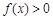 ,则
,则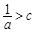 ,
,
所以f(x)在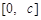 上是单调递减的,且在
上是单调递减的,且在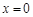 处取到最大值1, ………12分
处取到最大值1, ………12分
要使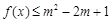 ,对所有
,对所有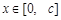 恒成立,
恒成立,
必须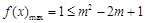 成立,
成立,
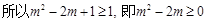 ,
,
解得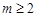 或
或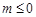 , 而
, 而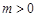 ,
,
所以m的最小值为2. ………16分
【解析】略

练习册系列答案
相关题目
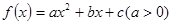 的图象与
的图象与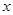 轴有两个不同公共点,若
轴有两个不同公共点,若
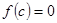 ,且当
,且当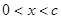 时,
时, 。
。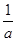 与
与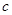 的大小。
的大小。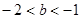
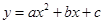 的图象与x交于点(-2,0)、(
的图象与x交于点(-2,0)、(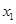 ,0),且1<
,0),且1<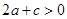 ③
③ ④
④ 其中正确结论的个数是( )
其中正确结论的个数是( )