题目内容
19.已知M(-1,2),N(2,-2),若动点P(x,y)满足|PM|+|PN|=5,则$\frac{y+2}{x}$的取值范围为(-∞,-4]∪[0,+∞).分析 运用两点的距离公式,可得P的轨迹为线段MN,$\frac{y+2}{x}$的几何意义是P(x,y)与A(0,-2)的斜率,结合图形,即可得到所求范围.
解答 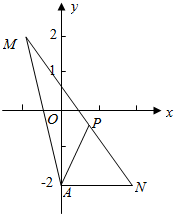 解:M(-1,2),N(2,-2),
解:M(-1,2),N(2,-2),
可得|MN|=$\sqrt{(-1-2)^{2}+(2+2)^{2}}$=5,
即有|PM|+|PN|=5=|MN|,
P的轨迹为线段MN,
则$\frac{y+2}{x}$的几何意义是P(x,y)与A(0,-2)的斜率,
由图象可得kAM=$\frac{2+2}{-1-0}$=-4,kAN=$\frac{-2+2}{2-0}$=0,
即有$\frac{y+2}{x}$的取值范围为(-∞,-4]∪[0,+∞).
故答案为:(-∞,-4]∪[0,+∞).
点评 本题考查动点的轨迹方程的求法,注意运用直线的斜率公式,结合图形观察,属于中档题.

练习册系列答案
相关题目
7.已知函数y=f(x)=$\left\{\begin{array}{l}{5x,0<x≤13}\\{7x+2,x>13}\end{array}\right.$的定义域是( )
| A. | (0.+∞) | B. | (-∞,0]∪[0,+∞) | C. | (-∞,0]∪(0,+∞) | D. | [0,+∞) |
19.已知f(x)=ax4+bx2-x+m,f(2)=1,则f(-2)=( )
| A. | 5 | B. | 0 | C. | 3 | D. | -2 |
 如图所示,△ABC中,AC=10cm,AC边上的高BD=10cm,求其水平放置的直观图的面积.
如图所示,△ABC中,AC=10cm,AC边上的高BD=10cm,求其水平放置的直观图的面积.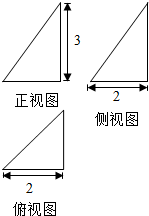 一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.
一个几何体的三视图是三个直角三角形,尺寸如图所示,求表面积.