Question

设P（a，b）、R（a，2）为坐标平面xoy上的点，直线OR（O为坐标原点）与抛物线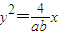交于点Q（异于O）．
（1）若对任意ab≠0，点Q在抛物线y=mx²+1（m≠0）上，试问当m为何值时，点P在某一圆上，并求出该圆方程M；
（2）若点P（a，b）（ab≠0）在椭圆x²+4y²=1上，试问：点Q能否在某一双曲线上，若能，求出该双曲线方程，若不能，说明理由；
（3）对（1）中点P所在圆方程M，设A、B是圆M上两点，且满足|OA|•|OB|=1，试问：是否存在一个定圆S，使直线AB恒与圆S相切．

Answer 1

【答案】分析：（1）把直线方程与抛物线方程联立求得交点Q的坐标，代入y=mx²+1，求得a和b的关系式，进而判断出当m=1时，点P（a，b）在圆M：x²+（y-1）²=1上
（2）设，进而根据点Q的坐标，求得y₂^Q-mx₂^Q=16，进而判断出，点Q在双曲线y²-4x²=16上．
（3）设AB：x=ky+λ，A（x₁，y₁），B（x₂，y₂），进而根据|OA|•|OB|=1，求得y₂•y₁，进而把直线与圆方程联立，求得y₂•y₁，进而根据原点O到直线AB距离求得d，进而判断出直线AB恒与圆相切．
解答：解：（1）∵，
代入⇒ma²+b²-2b=0
当m=1时，点P（a，b）在圆M：x²+（y-1）²=1上
（2）∵P（a，b）在椭圆x²+4y²=1上，即a²+（2b）²=1
∴可设
又∵，
∴=（令m=4）
∴点Q在双曲线y²-4x²=16上
（3）∵圆M的方程为x²+（y-1）²=1
设AB：x=ky+λ，A（x₁，y₁），B（x₂，y₂），由|OA|•|OB|=1⇒
又∵⇒（k²+1）y²+2（kλ-1）y+λ²=0，
∴
又原点O到直线AB距离
∴，即原点O到直线AB的距离恒为
∴直线AB恒与圆相切．
点评：本题主要考查了直线与圆锥曲线的综合问题．直线与圆锥曲线的综合问题能有效地考查考生分析问题、解决问题的能力，因此倍受高考命题人的青睐．