题目内容
设函数 .
.
(1)求 的单调区间;
的单调区间;
(2)若存在区间 ,使
,使 在
在 上的值域是
上的值域是 ,求
,求 得取值范围.
得取值范围.
解:(1)由题意得,函数 的定义域是
的定义域是 ,
, ,令
,令 则
则 ,当
,当 即
即 时,函数
时,函数 单调递减;当
单调递减;当 即
即 时,函数
时,函数 单调递增,所以
单调递增,所以 在
在 上单调递减,在
上单调递减,在 上单调递增,则
上单调递增,则 的最小值为
的最小值为 ,所以
,所以 ,即
,即 的单调递增区间是
的单调递增区间是 .…………6分
.…………6分
(2)由(1)得 在区间
在区间 上单调递增,又
上单调递增,又 在
在 上的值域是
上的值域是 ,所以
,所以 其中
其中 ,
,
从而 ,由
,由 得
得 ,
,
令 ,则
,则 ,
,
令 则
则 ,
,
所以 在
在 上单调递增,
上单调递增, ,
,
当 时,
时, ,所以
,所以 ,
,
当 时,
时, ,所以
,所以 ,
,
所以 在
在 上单调递增,在
上单调递增,在 上单调递增,所以
上单调递增,所以 的最小值为
的最小值为 ,
,
故由题意可知 ,解得
,解得 ,
,
即 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
 中,
中, 为
为 的中点,点
的中点,点 在线段
在线段 上运动,则
上运动,则 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.
 的图象与直线
的图象与直线 的交点为
的交点为 的图象与直线
的图象与直线 的交点为
的交点为 ,
, 恰好是点
恰好是点 的值是 .
的值是 . ,则下列不等式成立的是( )
,则下列不等式成立的是( ) B.
B. C.
C. D.
D.
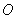 为线段
为线段 外一点,若
外一点,若 Hong任意相邻两点的距离相等,
Hong任意相邻两点的距离相等, ,
, ,用
,用 表示
表示 其结果为( )
其结果为( ) B.
B.
 D.
D.

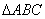 中,
中, 是边
是边 上的点,若
上的点,若 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 且与直线
且与直线 平行的直线方程是( )
平行的直线方程是( ) B.
B. C.
C. D.
D.