题目内容
【题目】已知函数![]() .
.
(Ⅰ)设![]() 是
是![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,![]() 在定义域内恒成立,求
在定义域内恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,证明:
时,证明:![]() .
.
【答案】(Ⅰ)1(Ⅱ)2(Ⅲ)详见解析
【解析】
(Ⅰ)对函数![]() 求导,由题意知
求导,由题意知![]() ,可求出
,可求出![]() 的值,经检验m=1符合题意;(Ⅱ)求出函数
的值,经检验m=1符合题意;(Ⅱ)求出函数![]() 的单调性,进而求出最小值
的单调性,进而求出最小值![]() ,令
,令![]() 即可得到答案;(Ⅲ)由题意,当m≤2,x∈(-m,+∞)时,
即可得到答案;(Ⅲ)由题意,当m≤2,x∈(-m,+∞)时,![]() ,故只需证明当m=2时,
,故只需证明当m=2时,![]() ,进而分析函数单调性,求得
,进而分析函数单调性,求得![]() ,即可。
,即可。
解:(Ⅰ)∵![]() ,x=0是f(x)的极值点,∴
,x=0是f(x)的极值点,∴![]() ,解得m=1.
,解得m=1.
经检验m=1符合题意.
(Ⅱ)由( Ι)可知,函数f(x)=ex-ln(x+1)+1,其定义域为(-1,+∞).
∵![]()
设g(x)=ex(x+1)-1,则g′(x)=ex(x+1)+ex>0,所以g(x)在(-1,+∞)上为增函数,
又∵g(0)=0,所以当x>0时,g(x)>0,即f′(x)>0;当-1<x<0时,g(x)<0,f′(x)<0.
所以f(x)在(-1,0)上为减函数;在(0,+∞)上为增函数;因此,![]() 的最小值为
的最小值为![]()
∵![]() 在定义域内恒成立,即
在定义域内恒成立,即![]()
(Ⅲ)证明:要证![]() ,即
,即![]() .
.
设![]() ,即证
,即证![]()
当m![]() ,故只需证明当m=2时,
,故只需证明当m=2时,![]() .
.
当m=2时,函数![]() 在(-2,+∞)上为增函数,且
在(-2,+∞)上为增函数,且![]() .
.
故![]() 在(-2,+∞)上有唯一实数根
在(-2,+∞)上有唯一实数根![]() ,且
,且![]() ∈(-1,0).
∈(-1,0).
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
从而当![]() 时,
时,![]() 取得最小值.
取得最小值.
由![]() ,得
,得![]() ,即
,即![]() ,故
,故![]() .
.
综上,当m≤2时,![]() 即
即![]() >m.
>m.

【题目】有7位歌手(1至7号)参加一场歌唱比赛, 由550名大众评委现场投票决定歌手名次, 根据年龄将大众评委分为5组, 各组的人数如下:
组别 | A | B | C | D | E |
人数 | 50 | 100 | 200 | 150 | 50 |
(Ⅰ) 为了调查大众评委对7位歌手的支持状况, 现用分层抽样方法从各组中抽取若干评委, 其中从B组中抽取了6人. 请将其余各组抽取的人数填入下表.
组别 | A | B | C | D | E |
人数 | 50 | 100 | 200 | 150 | 50 |
抽取人数 | 6 |
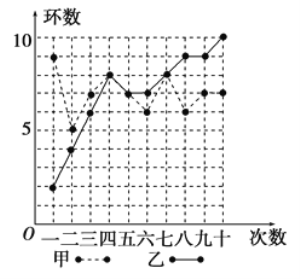
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
(2)从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中![]() 环及
环及![]() 环以上的次数相结合看(分析谁的成绩好些);
环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).