��Ŀ����
����Ŀ����ͼ��ij�����ڵ�·EF��һ����һ���˶���������������ǰһ����Ϊ���߶�FBC�������߶��Ǻ��� ![]() ��A��0���أ�0����x��[��4��0]ʱ��ͼ����ͼ�����ߵ�ΪB����1��2�����������м䲿��Ϊ��
��A��0���أ�0����x��[��4��0]ʱ��ͼ����ͼ�����ߵ�ΪB����1��2�����������м䲿��Ϊ�� ![]() ǧ��ֱ���ܵ�CD����CD��EF�������ĺ�һ��������OΪԲ�ĵ�һ��Բ��
ǧ��ֱ���ܵ�CD����CD��EF�������ĺ�һ��������OΪԲ�ĵ�һ��Բ�� ![]() ��
�� 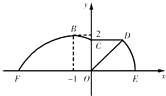
��1����ص�ֵ�͡�DOE�Ĵ�С��
��2����Ҫ��Բ����������Ӧ������ODE�����ڽ�һ�������β�ƺ�������ε�һ���ڵ�·EF�ϣ�һ�������ڰ뾶OD�ϣ�����һ������P��Բ�� ![]() �ϣ��ҡ�POE=�ȣ������β�ƺ�������ȡ���ֵʱ�ȵ�ֵ��
�ϣ��ҡ�POE=�ȣ������β�ƺ�������ȡ���ֵʱ�ȵ�ֵ��
���𰸡�
��1���⣺����������A=2�� ![]() ��
��
�� ![]() ����
���� ![]() ��
��
�����߶�FBC�Ľ���ʽΪ ![]() ��
��
��x=0ʱ�� ![]() ����CD=
����CD= ![]() ����
���� ![]() ��
��
��2���⣺�ɣ�1������֪ ![]() ��
��
����֪�������β�ƺ����������ʱ����P�ڻ�DE�ϣ��� ![]() ��
��
���POE=�ȣ� ![]() �������β�ƺ�������Ϊ
�������β�ƺ�������Ϊ ![]()
= ![]() ��
��
�� ![]() ����
���� ![]() ȡ�����ֵ
ȡ�����ֵ
����������1�������⣬��A=2�� ![]() ���������ڹ�ʽT=
���������ڹ�ʽT= ![]() �ɵæأ���B�������������֪�ɵæգ��Ӷ������DOE�Ĵ�С����2���ɣ�1����֪OD=OP�����β�ƺ�����S���ڦȵĺ�������
�ɵæأ���B�������������֪�ɵæգ��Ӷ������DOE�Ĵ�С����2���ɣ�1����֪OD=OP�����β�ƺ�����S���ڦȵĺ������� ![]() ��������Һ��������ʿ���Sȡ�����ֵ��
��������Һ��������ʿ���Sȡ�����ֵ��
�����㾫�����������⣬������Ҫ�˽����Ǻ�������ֵ(����![]() ����
����![]() ʱ��ȡ����СֵΪ
ʱ��ȡ����СֵΪ![]() ����
����![]() ʱ��ȡ�����ֵΪ
ʱ��ȡ�����ֵΪ![]() ����
����![]() ��
��![]() ��
��![]() )��
)��
