题目内容
已知函数 .
.
(Ⅰ)求函数 最大值和最小正周期;
最大值和最小正周期;
(Ⅱ)设 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,若
,若 ,求
,求 的值
的值
 .
.(Ⅰ)求函数
 最大值和最小正周期;
最大值和最小正周期;(Ⅱ)设
 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,若
,若 ,求
,求 的值
的值(Ⅰ) 的最大值为0,最小正周期是
的最大值为0,最小正周期是 ;(Ⅱ)
;(Ⅱ) ,
, .
.
 的最大值为0,最小正周期是
的最大值为0,最小正周期是 ;(Ⅱ)
;(Ⅱ) ,
, .
.试题分析:(Ⅰ)先化简
 ,再求函数
,再求函数 最大值和最小正周期;(Ⅱ)根据正弦定理化简
最大值和最小正周期;(Ⅱ)根据正弦定理化简 ,由余弦定理得
,由余弦定理得 ,通过解方程求解答案.
,通过解方程求解答案.试题解析:
(Ⅰ)
 , (3分)
, (3分)则
 的最大值为0,最小正周期是
的最大值为0,最小正周期是 . (5分)
. (5分)(Ⅱ)
 ,则
,则 . (6分)
. (6分)∵
 ,∴
,∴ ,∴
,∴ ,
,∴
 ,∴
,∴ . (7分)
. (7分)又∵
 ,由正弦定理得
,由正弦定理得 ,① (9分)
,① (9分)由余弦定理得
 ,即
,即 ,② (10分)
,② (10分)由①②解得
 ,
, . (12分)
. (12分)
练习册系列答案
相关题目
 =
= .
. ,求
,求 的值。
的值。 。
。 的单调区间;
的单调区间; =1,BC=2,B=
=1,BC=2,B= ,求AC边的长.
,求AC边的长. ,
, 是第三象限的角,则
是第三象限的角,则
 = ( )
= ( )



 为
为 的内角
的内角 的对边,满足
的对边,满足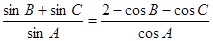 ,函数
,函数
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减. ;
; ,证明
,证明 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,则
,则 ,
, .
. ,则
,则 .
. ,
, ,则
,则 的值为( )
的值为( )


