题目内容
(本小题满分14分)设函数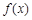 的定义域是R,对于任意实数
的定义域是R,对于任意实数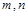 ,恒有
,恒有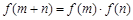 ,且当
,且当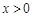 时,
时,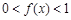 .
.
(Ⅰ)若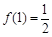 ,求
,求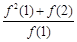 的值;(Ⅱ)求证:
的值;(Ⅱ)求证: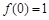 ,且当
,且当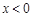 时,有
时,有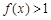 ;
;
(Ⅲ)判断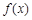 在R上的单调性,并加以证明.
在R上的单调性,并加以证明.
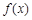 的定义域是R,对于任意实数
的定义域是R,对于任意实数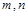 ,恒有
,恒有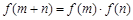 ,且当
,且当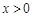 时,
时,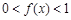 .
.(Ⅰ)若
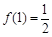 ,求
,求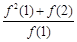 的值;(Ⅱ)求证:
的值;(Ⅱ)求证: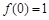 ,且当
,且当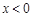 时,有
时,有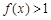 ;
;(Ⅲ)判断
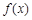 在R上的单调性,并加以证明.
在R上的单调性,并加以证明.解:(Ⅰ)令m=n=1得f(2)=f(1)f(1)=
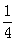 , 2分
, 2分∴
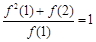 . 4分
. 4分(Ⅱ)
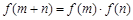 ,
,令
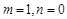 ,则
,则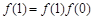 ,且当
,且当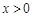 时,
时,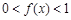 ,
,∴
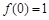 ; 6分
; 6分设
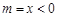 ,
,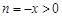 ,
,∴
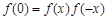 ,∴
,∴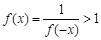 . 9分
. 9分(Ⅲ)在R上任取x1,x2,使得
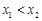 ,
,则
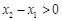 ,∴
,∴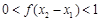 ,
,∴
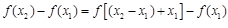
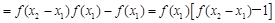
∵当x>0时,0<f(x)<1;当x=0时,f(x)=1>0;当x<0时,f(x) >1
∴对任意x∈R,有f(x) >0,∴f(x1)>0
∵0<f(x2-x1)<1 ∴f(x2-x1)-1<0
∴f(x2)-f(x1)<0,即f(x1)>f(x2)
∴
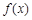 在R上是单调递减. 14分
在R上是单调递减. 14分略

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
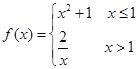 ,则f(f(10)=
,则f(f(10)=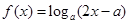 在区间
在区间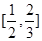 上恒有
上恒有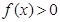 ,则实数
,则实数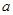 的取值范围是 。
的取值范围是 。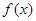 的导函数为
的导函数为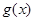 ,且满足:①
,且满足:①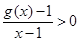 ,②
,②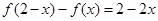 ,记
,记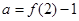 ,
,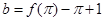 ,
,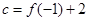 ,则
,则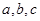 的大小顺序为( )
的大小顺序为( )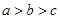 B.
B. 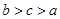 C.
C. 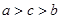 D.
D. 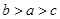
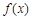 满足
满足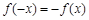 ,
,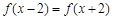 ,且
,且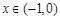 时,
时,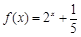 则
则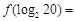 __________
__________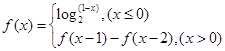 则f(2011)的值为
则f(2011)的值为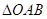 是边长为2的正三角形,记
是边长为2的正三角形,记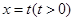 左侧的图形的面积为
左侧的图形的面积为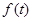 .
. 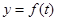 的图像;
的图像;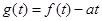 有且只有一个零点时,求
有且只有一个零点时,求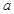 的值.
的值.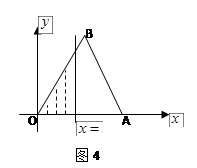
 的最小值为
的最小值为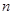 ,则二项式
,则二项式 的展开式中常数项为第 项。
的展开式中常数项为第 项。 为
为 上的偶函数,且满足
上的偶函数,且满足 ,
, ,
, ,则
,则