题目内容
【题目】a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：
①当直线AB与a成60°角时，AB与b成30°角；
②当直线AB与a成60°角时，AB与b成60°角；
③直线AB与a所成角的最小值为45°；
④直线AB与a所成角的最小值为60°；
其中正确的是（填写所有正确结论的编号）
【答案】②③
【解析】解：由题意知，a、b、AC三条直线两两相互垂直，画出图形如图，
不妨设图中所示正方体边长为1，
故|AC|=1，|AB|= 
，
斜边AB以直线AC为旋转轴，则A点保持不变，
B点的运动轨迹是以C为圆心，1为半径的圆，
以C坐标原点，以CD为x轴，CB为y轴，CA为z轴，建立空间直角坐标系，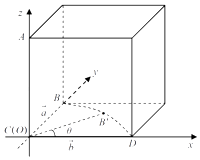
则D（1，0，0），A（0，0，1），直线a的方向单位向量 
=（0，1，0），| |=1，
直线b的方向单位向量 
=（1，0，0），| |=1，
设B点在运动过程中的坐标中的坐标B′（cosθ，sinθ，0），
其中θ为B′C与CD的夹角，θ∈[0，2π），
∴AB′在运动过程中的向量， 
=（﹣cosθ，﹣sinθ，1），| |= ，
设 与 所成夹角为α∈[0， 
]，
则cosα= 
= 
|sinθ|∈[0， ]，
∴α∈[ 
， ]，∴③正确，④错误．
设 与 所成夹角为β∈[0， ]，
cosβ=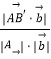 
= 
= |cosθ|，
当 与 夹角为60°时，即α= 
，
|sinθ|= 
= 
= ，
∵cos2θ+sin2θ=1，∴cosβ= |cosθ|= 
，
∵β∈[0， ]，∴β= ，此时 与 的夹角为60°，
∴②正确，①错误．
故答案为：②③．
由题意知，a、b、AC三条直线两两相互垂直，构建如图所示的边长为1的正方体，|AC|=1，|AB|= ，斜边AB以直线AC为旋转轴，则A点保持不变，B点的运动轨迹是以C为圆心，1为半径的圆，以C坐标原点，以CD为x轴，CB为y轴，CA为z轴，建立空间直角坐标系，利用向量法能求出结果．
