Question

【题目】已知函数， （为常数）.

（1）函数的图象在点处的切线与函数的图象相切，求实数的值；

（2）若函数在定义域上存在单调减区间，求实数的取值范围；

（3）若， ，且，都有成立，求实数的取值范围.

Answer 1

【答案】（1）（2）（3）

【解析】试题分析: (1)求出函数的图象在点的切线方程,再由直线与抛物线相切, ,求出实数的值; (2)由题意构造函数 ,求出, 在上有解,再由二次函数相关知识求出的范围; (3)假定 ,先分别求出函数在上的单调性,将原不等式转化为,即在上为增函数,求出实数的范围.

试题解析:（1）因为，所以，因此，

所以函数的图象在点处的切线方程为，

由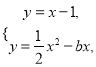得.

由，得.

（还可以通过导数来求）

（2）因为 ，

所以，

由题意知在上有解，

因为，设，因为，

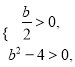则只要解得，

所以的取值范围是.

（3）不妨设，

因为函数在区间上是增函数，

所以，

函数图象的对称轴为，且.

当时，函数在区间上是减函数，

所以，

所以，

等价于，

即，

等价于 在区间上是增函数，

等价于在区间上恒成立，

等价于在区间上恒成立，所以，又，所以.

点睛: 本题主要考查导数的应用,包括导数的几何意义,导数与单调性,属于中档题.本题在第3问中注意解题思想:等价转换,将原不等式转化为求在上为增函数,等价于在区间上恒成立,分离出,转化为求在上的最小值.