题目内容
【题目】已知椭圆![]() .
.
(1)若椭圆![]() 的右焦点坐标为
的右焦点坐标为![]() ,求
,求![]() 的值;
的值;
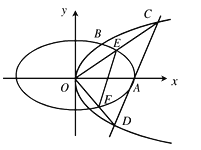
(2)由椭圆![]() 上不同三点构成三角形称为椭圆的内接三角形.若以
上不同三点构成三角形称为椭圆的内接三角形.若以![]() 为直角顶点的椭圆
为直角顶点的椭圆![]() 的内接等腰直角三角形恰有三个,求
的内接等腰直角三角形恰有三个,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)本问考查椭圆标准方程,先将椭圆方程化为标准形式, 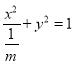 ,根据右焦点为
,根据右焦点为![]() ,则
,则![]() ,可以求出
,可以求出![]() 的值;(2)本问考查直线与椭圆位置关系,由题分析
的值;(2)本问考查直线与椭圆位置关系,由题分析![]() ,则
,则![]() ,因此BA所在直线斜率存在且不为0,可设
,因此BA所在直线斜率存在且不为0,可设![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立,根据弦长公式求出
,将直线方程与椭圆方程联立,根据弦长公式求出![]() ,同理BC所在直线方程为
,同理BC所在直线方程为![]() ,同理求出
,同理求出![]() ,根据等腰直角三角形有
,根据等腰直角三角形有![]() ,整理得到关于
,整理得到关于![]() 的关系式,转化为以
的关系式,转化为以![]() 为变量的方程有两个不相等的正实根问题,求
为变量的方程有两个不相等的正实根问题,求![]() 的取值范围.
的取值范围.
试题解析:(1)椭圆![]() 的方程可以写成
的方程可以写成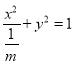 ,因为焦点
,因为焦点![]() 在
在![]() 轴上,所以
轴上,所以![]() ,求得
,求得![]() .
.
(2)设椭圆![]() 内接等腰直角三角形的两直角边分别为
内接等腰直角三角形的两直角边分别为![]() 设
设![]() ,显然
,显然![]() 与
与![]() 不与坐标轴平行,且
不与坐标轴平行,且![]() ,所以可设直线
,所以可设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,由
,由![]() ,消去
,消去![]() 得到
得到![]() ,所以
,所以![]() ,求得
,求得![]() .同理可求
.同理可求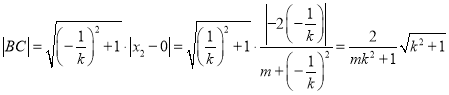 ,因为
,因为![]() 为以
为以![]() 为直角顶点的等腰直角三角形,所以
为直角顶点的等腰直角三角形,所以![]() .所以
.所以![]() ,整理得
,整理得
![]() ,所以
,所以![]() ,由此
,由此
![]() ,所以
,所以![]() 或
或![]() ,设
,设![]() ,因为以
,因为以![]() 为直角顶点的椭圆内接等腰直角三角形恰有三个,所以关于
为直角顶点的椭圆内接等腰直角三角形恰有三个,所以关于![]() 的方程
的方程![]() 有两个不同的正实根
有两个不同的正实根![]() ,且都不为
,且都不为![]() .所以
.所以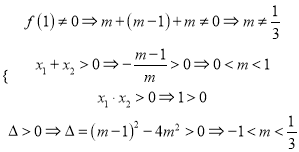 ,解得实数
,解得实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目