Question

【题目】【2015高考湖北（理）20】某厂用鲜牛奶在某台设备上生产两种奶制品．生产1吨产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨产品需鲜牛奶1.5吨，使用设备1.5小时，获利1200元．要求每天产品的产量不超过产品产量的2倍，设备每天生产两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W（单位：吨）是一个随机变量，其分布列为

W	12	15	18
P	0.3	0.5	0.2

该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利（单位：元）是一个随机变量．

（Ⅰ）求的分布列和均值；

（Ⅱ） 若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．

Answer 1

【答案】（Ⅰ）的分布列为：

	8160	10200	10800
	0.3	0.5	0.2

；（Ⅱ）0.973.

【解析】（Ⅰ）设每天两种产品的生产数量分别为，相应的获利为，

则有 （1）

目标函数为 ．

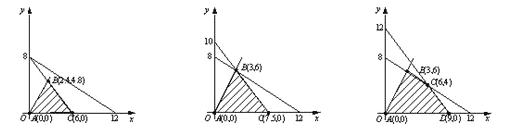
当时，（1）表示的平面区域如图1，三个顶点分别为．

将变形为，

当时，直线：在轴上的截距最大，

最大获利．

当时，（1）表示的平面区域如图2，三个顶点分别为．

将变形为，

当时，直线：在轴上的截距最大，

最大获利．

当时，（1）表示的平面区域如图3，

四个顶点分别为.

将变形为，

当时，直线：在轴上的截距最大，

最大获利．

故最大获利的分布列为

	8160	10200	10800
	0.3	0.5	0.2

因此，

（Ⅱ）由（Ⅰ）知，一天最大获利超过10000元的概率，

由二项分布，3天中至少有1天最大获利超过10000元的概率为