Question

定义在R上的函数满足f（0）=0，f（x）+f（1-x）=1，，且当0≤x₁＜x₂≤1时，f（x₁）≤f（x₂），则=________．

Answer 1

分析：先由已知条件f（0）=0，f（x）+f（1-x）=1，求出一些特值，f（1）=1，，可得f（）=，
再由当0≤x₁＜x₂≤1时，f（x₁）≤f（x₂），结合=f（）可以看出x∈时，f（x）=，
再利用条件将逐步转化到内，代入求解即可．
解答：由f（x）+f（1-x）=1可知f（x）的图象关于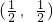对称，
由f（0）=0得f（1）=1，，
中令x=1可得f（）=，
又因为0≤x₁＜x₂≤1时，f（x₁）≤f（x₂），
所以x∈时，f（x）=，
由可得=，
因为，
所以，
所以
故答案为：
点评：本题考查抽象函数的性质的应用问题及转化思想，综合性较强，难度较大．