题目内容
如图3，在直三棱柱ABC—A1B1C1中，AB1⊥BC1,AB=CC1=1,BC=2.
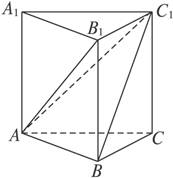
(1)求证：A1C1⊥AB；
(2)求点B1到平面ABC1的距离.
（1）见解析 （2） d=
解析:
(1)证明：连结A1B，则A1B⊥AB1.又∵AB1⊥BC1,∴AB1⊥平面A1BC1.
∴AB1⊥A1C1.又∵A1C1⊥BB1,∴A1C1⊥平面ABB1.∴A1C1⊥AB.
(2)解：由(1)知AB⊥AC，∵AB⊥AC1,又∵AB=1,BC=2，∴AC=
,AC1=2.
∴
=1.设所求距离为d，∴
.
∴
S△ABC1·d=
·A1C1.=·1·d=·
·. ∴d=
.
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
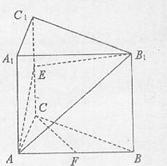
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，E是棱CC1上动点，F是AB中点，AC=BC=2，AA1=4．
，E是棱CC1上动点，F是AB中点，
；
，E是棱CC1上动点，F是AB中点，
；
，E是棱CC1上动点，F是AB中点，
；