题目内容
18.若f(x)=3sin(2ωx+$\frac{π}{6}$)-1在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增,则正实数ω的取值范围(0,$\frac{1}{2}$].分析 求出f(x)的增区间D,令[-$\frac{π}{6}$,$\frac{π}{3}$]⊆D,解出ω.
解答 解:令-$\frac{π}{2}$+2kπ≤2ωx+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,解得-$\frac{π}{3ω}$+$\frac{kπ}{ω}$≤x≤$\frac{π}{6ω}$+$\frac{kπ}{ω}$,
∵f(x)的单调递增区间为[-$\frac{π}{3ω}$+$\frac{kπ}{ω}$,$\frac{π}{6ω}$+$\frac{kπ}{ω}$],
∵f(x)在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增,
∴$\left\{\begin{array}{l}{-\frac{π}{3ω}≤-\frac{π}{6}}\\{\frac{π}{3}≤\frac{π}{6ω}}\end{array}\right.$,解得ω≤$\frac{1}{2}$.
∴又ω>0,∴0<ω$≤\frac{1}{2}$.
故答案为(0,$\frac{1}{2}$].
点评 本题考查了正弦函数的图象与性质,正弦函数的单调性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知A(1,2),B(5,4),C(x,3),D(-3,y),且$\overrightarrow{AB}$=$\overrightarrow{CD}$,则x,y的值分别为( )
| A. | -7,-5 | B. | 7,-5 | C. | -7,5 | D. | 7,5 |
3.袋中有2个红色的变形金刚,2个白色的变形金刚,2个黑色的变形金刚,从里面任意取2个变形金刚,不是基本事件的为( )
| A. | {恰好2个红色的变形金刚} | B. | {恰好2个黑色的变形金刚} | ||
| C. | {恰好2个白色的变形金刚} | D. | {至少1个红色的变形金刚} |
10.设复数z1=$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$i,z2=3+4i,则$\frac{{|z}_{1}^{2016}|}{|\overline{{z}_{2}}|}$=( )
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
7.非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2,<$\overrightarrow{a}$,$\overrightarrow{b}$>=30°,且对?λ>0,且|$\overrightarrow{a}$-λ$\overrightarrow{b}$|≥|$\overrightarrow{a}$-$\overrightarrow{b}$|恒成立,则$\overrightarrow{a}$•$\overrightarrow{b}$=( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
6.已知命题p:$\frac{1}{x-1}$<1,q:x2+(a-1)x-a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
| A. | (-2,-1] | B. | [-2,-1] | C. | [-3,-1] | D. | [-2,+∞) |
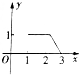
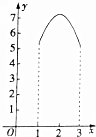
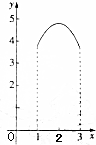
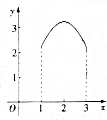
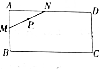 如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( )
如图,矩形ABCD的周长为8,设AB=x(1≤x≤3),线段MN的两端点在矩形的边上滑动,且MN=1,当N沿A→D→C→B→A在矩形的边上滑动一周时,线段MN的中点P所形成的轨迹为G,记G围成的区域的面积为y,则函数y=f(x)的图象大致为( )