题目内容
已知函数 的值域为C,则( )
的值域为C,则( )A.0∈C
B.-1∈C
C.3∈C
D.1∈C
【答案】分析:将函数f(x)化简整理,得f(x)=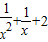 ,令
,令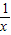 =t,转化为关于t的二次函数进行研究,可得函数的值域C=[
=t,转化为关于t的二次函数进行研究,可得函数的值域C=[ ,+∞),再将各选项与值域进行对照,即可得到本题的答案.
,+∞),再将各选项与值域进行对照,即可得到本题的答案.
解答:解: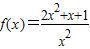 =
=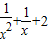
令t=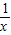 ,得f(x)=t2+t+2(t≠0)
,得f(x)=t2+t+2(t≠0)
∵t2+t+2=(t+ )2+
)2+ ≥
≥
∴f(x)的最小值为 ,相应的x=-2
,相应的x=-2
可得函数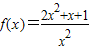 的值域C=[
的值域C=[ ,+∞)
,+∞)
由此对照各个选项,可得只有3∈[ ,+∞),其它各项均不符合
,+∞),其它各项均不符合
故选:C
点评:本题采用换元的方法,求分式函数的值域,着重考查了二次函数的图象与性质和函数值域求法等知识,属于基础题.
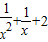 ,令
,令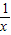 =t,转化为关于t的二次函数进行研究,可得函数的值域C=[
=t,转化为关于t的二次函数进行研究,可得函数的值域C=[ ,+∞),再将各选项与值域进行对照,即可得到本题的答案.
,+∞),再将各选项与值域进行对照,即可得到本题的答案.解答:解:
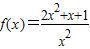 =
=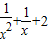
令t=
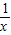 ,得f(x)=t2+t+2(t≠0)
,得f(x)=t2+t+2(t≠0)∵t2+t+2=(t+
 )2+
)2+ ≥
≥
∴f(x)的最小值为
 ,相应的x=-2
,相应的x=-2可得函数
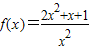 的值域C=[
的值域C=[ ,+∞)
,+∞)由此对照各个选项,可得只有3∈[
 ,+∞),其它各项均不符合
,+∞),其它各项均不符合故选:C
点评:本题采用换元的方法,求分式函数的值域,着重考查了二次函数的图象与性质和函数值域求法等知识,属于基础题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 的值域为
的值域为 ,则( )
,则( ) B.
B. C.
C. D.
D.
 的值域为C,则
的值域为C,则 的值域为C,则( )
的值域为C,则( )