题目内容
设函数f0(x)＝1－x2，f1(x)＝
，fn(x)＝
，(n≥1，n≥N)，则方程f1(x)＝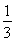
有________个实数根，方程fn(x)＝
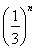有________个实数根．
4，2n＋1
【解析】f1(x)＝
，∴x2＝
或x2＝
有4个解．
∵可推出n＝1，2，3…，根个数分别为22，23，24，
∴通过类比得出fn(x)＝
有2n＋1个实数根．
练习册系列答案
相关题目
题目内容
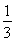设函数f0(x)＝1－x2，f1(x)＝，fn(x)＝，(n≥1，n≥N)，则方程f1(x)＝有________个实数根，方程fn(x)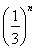＝有________个实数根．
4，2n＋1
【解析】f1(x)＝，∴x2＝或x2＝有4个解．
∵可推出n＝1，2，3…，根个数分别为22，23，24，
∴通过类比得出fn(x)＝有2n＋1个实数根．
