题目内容
实数x,y满足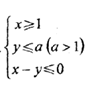
，若函数z=x+y的最大值为4,则实数a的值为( )
| A．2 | B．3 | C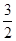． | D．4 |
A
解析试题分析：由
，得
,则
表示该组平行直线在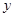
轴的截距。又由约束条件
作出可行域如图，先画出
，经平移至经过
和
的交点
时，取得最大值，代入，即
，所以
，故选
.
考点：线性规划求目标函数的最值.
练习册系列答案
相关题目
已知实数
满足不等式组
则目标函数
的最小值
与最大值
的积为()
A． | B． | C． | D． |
设变量
满足
，则
的最大值和最小值分别为（ ）
| A．1，-1 | B．2，-2 | C．1，-2 | D．2，-1 |
已知
满足约束条件
，则目标函数
的最大值（ ）
A． | B． | C． | D． |
若原点和点
分别在直线
的两侧，则
的取值范围是
A． | B． | C． 或 | D． 或 |
已知函数
的图像如图所示，则
的取值范围是（ ）
A． | B． | C． | D． |
设变量
满足条件
则点
所在区域的面积为（ ）
| A．4 | B．6 | C．8 | D．10 |
已知变量x,y满足约束条件
，则z=x+2y的最小值为
| A．3 | B．1 | C．-5 | D．-6 |
某旅行社租用A，B两种型号的客车安排900名客人旅行，A，B两种车辆的载客量分别为36人和60人，租金分别为1600元/辆和2400元/辆，旅行社要求租车总数不超过21辆，且B型车不能多于A型车7辆，则租金最少为( )
| A．31 200元 | B．36 000元 | C．36 800元 | D．38 400元 |