Question

函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x).当x∈[0,1]时,f(x)=2x.若在区间[-2,2]上方程ax+a-f(x)=0恰有三个不相等的实数根,则实数a的取值范围是　　　　. 

Answer 1

解析:由f(x+2)=f(x)得函数的周期是2.

由ax+a-f(x)=0得f(x)=ax+a,

设y=f(x),y=ax+a,作出函数y=f(x),y=ax+a的图象.

如图,要使方程ax+a-f(x)=0恰有三个不相等的实数根,

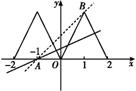
则直线y=ax+a=a(x+1)的斜率满足0≤a<k_AB,

由题意可知,A(-1,0),B(1,2),

所以k_AB==1,

所以0≤a<1,

即a∈[0,1).

答案:[0,1)