题目内容
确定函数f(x)=
解析:由已知得f′(x)=![]() ,令f′(x)=0,解得x=-1或x=1.列出下表:
,令f′(x)=0,解得x=-1或x=1.列出下表:
x | -2 | (-2,-1) | -1 | (-1,1) | 1 | (1,2) | 2 |
f′(x) |
| - | 0 | + | 0 | - |
|
f(x) |
|
| 极小值 |
| 极大值 |
|
|
由表可知:f(x)的极小值是f(-1)=![]() ;极大值是f(1)=
;极大值是f(1)=![]() .
.
又f(-2)=-![]() ,f(2)=
,f(2)=![]() ,
,
∴f(x)在区间[-2,2]上的最大值是![]() ,最小值是-
,最小值是-![]() .
.
温馨提示
即函数f(x)=![]() 的定义域为R.又∵
的定义域为R.又∵![]() =0,
=0,
∴f(x)在R上的最大值与最小值还分别为![]() 和-
和-![]() .
.
又f(0)=0,
∴函数f(x)= ![]() 在R上的值域为[-
在R上的值域为[-![]() ,
,![]() ].
].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
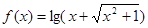 .
.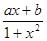 是定义在(-1,1)上的奇函数,且f(
是定义在(-1,1)上的奇函数,且f(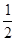 )=
)=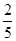 .
.