题目内容
已知A、B、C的坐标分别为A（4，0）、B（0，4）、C（3cosα，3sinα）（Ⅰ）若a∈（-π，0），且|
|=|
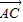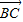|．求角α的值；（Ⅱ）若
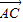
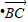=0．求
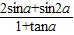的值．
【答案】分析：（Ⅰ）求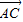
与
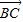向量，利用向量的模相等．得到方程即可求角α的值；
（Ⅱ）通过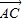
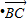=0．化简得到关系式，然后找出与求
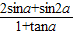的值有关的函数值即可求解．
解答：解：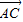
=（3cosα-4，3sinα）；
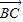=（3cosα，3sinα-4）…（2分）
（Ⅰ）|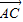
|=|
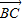|．得（3cosα-4）2+9sin2α=9cos2α+（3sinα-4）2，
∴sinα=cosα…（5分）
因为a∈（-π，0），所以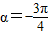
…（7分）
（Ⅱ）∵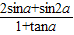
=
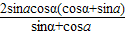=2sinαcosα…（9分）
∵
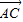
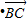=0，∴3cosα（3cosα-4）+3sinα（3sinα-4）=0…（11分）
∴sinα+cosα=
，两边平方可得：2sinαcosα=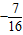
，
∴
=
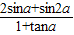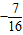…（13分）
点评：本题考查三角函数的化简求值，同角三角函数的基本关系式的应用，考查计算能力．
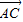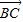与向量，利用向量的模相等．得到方程即可求角α的值；（Ⅱ）通过
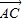
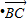=0．化简得到关系式，然后找出与求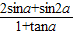的值有关的函数值即可求解．解答：解：
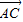=（3cosα-4，3sinα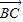）；=（3cosα，3sinα-4）…（2分）（Ⅰ）|
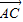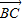|=||．得（3cosα-4）2+9sin2α=9cos2α+（3sinα-4）2，∴sinα=cosα…（5分）
因为a∈（-π，0），所以
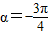…（7分）（Ⅱ）∵
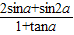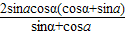==2sinαcosα…（9分）∵
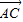
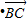=0，∴3cosα（3cosα-4）+3sinα（3sinα-4）=0…（11分）∴sinα+cosα=
，两边平方可得：2sinαcosα=，∴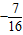
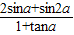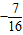=…（13分）点评：本题考查三角函数的化简求值，同角三角函数的基本关系式的应用，考查计算能力．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目