题目内容
已知函数y=f(x)对任意x,yÎR均有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,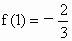 .
.
(1)判断并证明f(x)在R上的单调性;
(2)求f(x)在[-3,3]上的最大、小值.
答案:略
解析:
提示:
解析:
|
抽象函数的性质要紧扣定义,并同时注意特殊值的应用. 解: (1)令x=y=0,f(0)=0,令x=-y可得f(-x)=-f(x),在R上任取
∵ 又∵x>0时,f(x)<0,∴ 即 由定义可知f(x)在R上为单调递减函数. (2)∵f(x)在R上是减函数. ∴f(x)在[-3,3]上也是减函数. ∴f(-3)最大,f(3)最小. f(3)=f(2)+f(1)=f(1)+f(1)+f(1)
∴f(-3)=―f(3)=2. 即f(x)在[-3,3]上最大值为2,最小值为-2. |
提示:
|
①证明函数的单调性,必须用定义严格证明,不能用特殊值去检验,判断函数的最值,往往从单调性入手. ②对于本题所给的抽象函数的性质 f(x+y)=f(x)+f(y),可先找到它的一个原型函数f(x)=kx,又 ,可知 ,可知 ,进而可以帮助我们快速解题. ,进而可以帮助我们快速解题. |

练习册系列答案
相关题目
已知函数y=f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |
 ,则
,则 ,
, .
. ,
, .
. .
.