Question

首先指出下列函数是怎样复合的，然后求导:

（1）y=（2x－1）⁵；

（2）y=；

（3）y=.

Answer 1

解:（1）设u=2x－1，则y=u⁵.

y'_x= y'_u·u'_x=5u⁴·（2x－1）'

=5（2x－1）⁴ · 2=10（2x－1）⁴.

（2）设u=ax²+bx+c，则y=.

y'_x= y'_u·u'_x=（ax²+bx+c（2ax+b）

=.

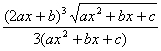（3）方法一:u=1－2x,y=u^－5.

∴y'_x= y'_u·u'_x=－5u^－6·（－2）

=10（1－2x）^－6.

方法二:y=,

令y=u⁵,u=，v=1－2x,

∴y'_x= y'_u·u'_v·v_x=5u⁴·（－v^－2）·（－2）

=10（）⁴·v^－2=10v^－6=10（1－2x）^－6.

点评:在用复合函数的求导法则求导数时，要把中间变量置换成原自变量的函数.