题目内容
已知关于x的不等式: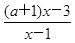 <1.
<1.
(1)当a=1时,解该不等式;
(2)当a为任意实数时,解该不等式.
(1){x|1<x<2};(2)详见解析.
解析试题分析:(1) 当a=1时,已知不等式化为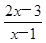 <1,进而可化为
<1,进而可化为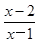 <0(特点:一边为一个分式,另一边为零)可写出不等式的解集; (2)由分式不等式的解法,先将已知不等式化为一边为一个分式,另一边为零的形式:
<0(特点:一边为一个分式,另一边为零)可写出不等式的解集; (2)由分式不等式的解法,先将已知不等式化为一边为一个分式,另一边为零的形式:  <0
<0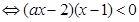 按a=0,a>0和a<0分类讨论,对于a>0,由于方程(ax-2)(x-1)=0的两根为x1=
按a=0,a>0和a<0分类讨论,对于a>0,由于方程(ax-2)(x-1)=0的两根为x1=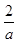 ,x2=1,所以又要按两根的大小分三类:大于、等于和小于进行讨论;对于a<0特别应注意写不等式的解集前先应将字母x的系数化为正.
,x2=1,所以又要按两根的大小分三类:大于、等于和小于进行讨论;对于a<0特别应注意写不等式的解集前先应将字母x的系数化为正.
试题解析:(1)当a=1时,不等式化为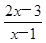 <1,化为
<1,化为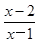 <0, .2分
<0, .2分
∴1<x<2,解集为{x|1<x<2} .5分
(2)a>0时,由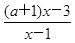 <1得
<1得 <0, 6分
<0, 6分
(ax-2)(x-1)<0,方程(ax-2)(x-1)=0的两根x1=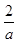 ,x2=1 8分
,x2=1 8分
当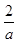 =1即a=2时,解集为
=1即a=2时,解集为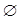 ; .9分
; .9分
当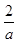 >1即0<a<2时,解集为
>1即0<a<2时,解集为 ; 11分
; 11分
当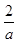 <1即a>2时,解集为
<1即a>2时,解集为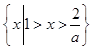 13分
13分
当a=0时,解集为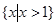
当a<0时,解集为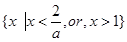
考点:分式不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,若对
,若对 是真命题,则实数
是真命题,则实数 的取值范围是 .
的取值范围是 .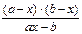 <0的解集是______.
<0的解集是______.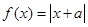 .
.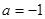 时,求不等式
时,求不等式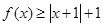 的解集;
的解集;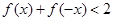 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围. ,(1)当a=2时,求关于x的不等式
,(1)当a=2时,求关于x的不等式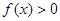 的解集;(2)当a>0时,求关于x的不等式
的解集;(2)当a>0时,求关于x的不等式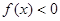 的解集.
的解集.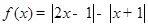 .
.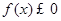 的解集
的解集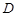 ;
;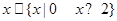 ,使得
,使得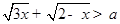 成立,求实数
成立,求实数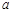 的取值范围.
的取值范围.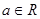 ,解关于
,解关于 的不等式
的不等式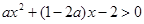 .
.