题目内容
记关于x的不等式| 3 | x |
(Ⅰ)求集合A;
(Ⅱ)求实数m的取值范围.
分析:(I)先通过移项通分将分式不等式化为一边为0且x的系数为正的形式,利用穿根求出解集即求出集合A.
(II)据B⊆A.分类讨论写出集合B,利用二次方程的判别式就B的各种情况求出m的范围.
(II)据B⊆A.分类讨论写出集合B,利用二次方程的判别式就B的各种情况求出m的范围.
解答:解:(Ⅰ)
>0?
<0?x(x-3)<0?0<x<3,
又∵x∈Z,∴A={1,2};
(Ⅱ)集合A={1,2}的子集有?、{1}、{2}、{1,2}.∵B⊆A,∴B=?;B={1}或{2};B={1,2}.
当B=?时,△=m2-8<0,解得-2
<m<2
.
当B={1}或{2}时,
或
,则m无解.
当B={1,2}时,
?
?m=3.
综上所述,实数m的取值范围是-2
<m<2
或m=3.
| 3-x |
| x |
| x-3 |
| x |
又∵x∈Z,∴A={1,2};
(Ⅱ)集合A={1,2}的子集有?、{1}、{2}、{1,2}.∵B⊆A,∴B=?;B={1}或{2};B={1,2}.
当B=?时,△=m2-8<0,解得-2
| 2 |
| 2 |
当B={1}或{2}时,
|
|
当B={1,2}时,
|
|
综上所述,实数m的取值范围是-2
| 2 |
| 2 |
点评:本题考查分式不等式的解法;利用集合的关系求集合;利用判别式判断二次方程根的情况.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
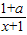 >1(a>0)的解集为P,函数f(x)=2x+log2(-x2+3x-2)的定义域为Q.
>1(a>0)的解集为P,函数f(x)=2x+log2(-x2+3x-2)的定义域为Q.